Rechnerische Lösungsverfahren von Bruchgleichungen
Letztendlich erhältst du auf jeden Fall nach dem Zusammenfassen, wenn du richtig gerechnet hast:
| 
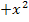
Jetzt fällt auch das x mit dem Quadrat heraus und du kannst die Gleichung leicht lösen.
| 
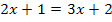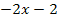
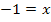
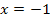
Nun noch einmal Vorsicht! Fällt dir etwas auf? Richtig! Der berechnete Wert x = – 1 liegt nicht in der Definitionsmenge D = ℚ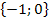 
und kann somit nicht die Lösung der Gleichung sein.
Schau´dir dazu noch einmal die gegebene Gleichung kurz an:
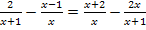
Bei x = – 1 ist ja genau die Definitionslücke der Gleichung, da wird der Nenner des ersten und letzten Bruchs gleich Null. Die Probe für x = – 1 können wir uns daher schenken. Die Lösungsmenge ist die leere Menge. Es gibt keine Lösung dieser Gleichung!
An dieser Aufgabe konntest du noch einmal schön sehen, dass es wirklich wichtig ist, die Definitionsmenge zu beachten. Hätten wir nämlich nicht an die Definitionsmenge gedacht und keine Probe gemacht, hätten wir x = – 1 für eine Lösung der Gleichung gehalten, was natürlich falsch wäre.
2. Verfahren:Gleichung auf die Form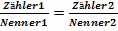 
bringen und dann kreuzweise multiplizieren
Wenn du diese Gleichung lieber erst auf beiden Seiten jeweils auf einen gemeinsamen Nenner bringen willst und dann durch kreuzweises Multiplizieren lösen möchtest, kannst du im Folgenden auch diesen zweiten Lösungsweg sehen.
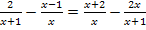
D = ℚ
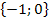
Wir überlegen uns den Hauptnenner der linken Seite, also den Hauptnenner der beiden Brüche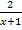 
und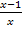 
. Der Hauptnenner dieser beiden Brüche ist natürlich x(x + 1).
Dann suchen wir den Hauptnenner der rechten Seite der Gleichung, also den Hauptnenner der Brüche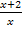 
und 
. Der Hauptnenner dieser beiden Brüche ist natürlich x(x + 1).
In diesem Fall ist der Hauptnenner der rechten Seite also identisch mit dem Hauptnenner der linken Seite der Gleichung. Das ist allerdings nicht immer so! Im Gegenteil, meist sind sie nicht gleich.
Jetzt erweitern wir so, dass die beiden Brüche, die jeweils auf der selben Seite der Gleichung stehen, auf einen gemeinsamen Nenner geschrieben werden können. So erhalten wir die Gleichung in der Form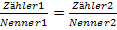 
.
Normalerweise, also wenn die Nenner auf beiden Seiten verschieden wären, würden wir jetzt kreuzweise multiplizieren. In diesem Fall entspricht dies aber auch einem Multiplizieren der gesamten Gleichung mit dem Hauptnenner, da hier der Nenner der linken Seite mit dem der rechten Seite übereinstimmt. Das bedeutet, dass in diesem Beispiel durch Zufall das kreuzweise Multiplizieren einem Multiplizieren mit dem Hauptnenner der gesamten Gleichung entspricht. In anderen Worten:Das 2. und 3. Verfahren laufen hier jeweils absolut identisch ab. Das ist übrigens bei allen Bruchgleichungen der Fall, deren Brüche auf der linken Seite der Gleichung den selben Hauptnenner haben, wie die auf der rechten Seite. Ob wir jetzt kreuzweise multiplizieren oder mit dem Hauptnenner der gesamten Gleichung, also mit x(x + 1), multiplizieren, läuft auf das Gleiche hinaus. Der Nenner fällt beim Kürzen komplett weg. Man kann eigentlich direkt die beiden Zähler miteinander gleichsetzen. Damit dir das wirklich klar wird, wird nun der Zwischenschritt des Multiplizierens mit dem Hauptnenner gezeigt. Wenn du selbst rechnest, kannst du den nächsten Schritt natürlich überspringen und sofort die Zähler gleichsetzen.
