Grenzwerte von e- und ln-Funktionen

Wir beginnen mit dem Verhalten für :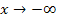

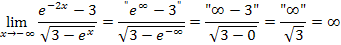
Für 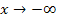liegt keine Asymptote vor.

Nun zum Verhalten von 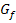bei linksseitiger Annäherung an die Stelle :

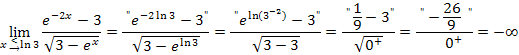
Falls dir dies nicht ganz klar ist, hier noch einmal alles ganz langsam:

Wir überlegen uns einzeln, wohin der Zähler bzw. der Nenner von 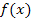für geht. Dazu setzen wir in Gedanken zuerst exakt die Zahl ln3 im Zähler und Nenner ein.

Im Zähler wenden wir im Exponenten von 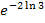das ln-Rechengesetz 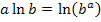an. Es gilt: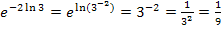

Diesen Term kannst du aber auch mit dem Taschenrechner berechnen. Einfach genau die Zahl ln3 in den Zähler von 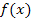, also in 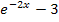, einsetzen und mit dem Taschenrechner ausrechnen, dann kommst du genauso darauf, dass der Zähler von 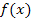gegen 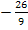geht.

Aber was ist mit dem Nenner vo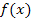n ? In 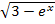setzen wir in Gedanken zuerst ebenfalls exakt die Zahl ln3 ein: 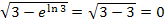So stellt man fest, dass der Nenner für gegen Null geht. Um das Vorzeichen der Null im Nenner zu ermitteln, kann man anschließend in Gedanken eine Zahl einsetzen, die etwas kleiner ist als ln3. (Man nimmt eine Zahl, die kleiner ist als ln3, wegen der Annäherung an ln3 von links. Dabei kannst du beispielsweise ln2,99 verwenden, das ist auf jeden Fall etwas kleiner als ln3. Weil die ln-Funktion streng monoton steigend ist, gilt:lna <lnb, wenn a <b.) Unter der Wurzel ergibt sich für auf jeden Fall eine positive Zahl, die fast Null ist. Für ergibt sich: (Die Null unter der Wurzel kann gar nicht 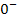sein, sonst wäre die Wurzel ja gar nicht definiert.) Das Ergebnis der Wurzel ist wiederum positiv;wir erhalten im Nenne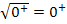r . Für gilt somit: 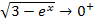Der Nenner geht also für gegen .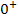

Nun wissen wir, dass der Zähler gegen die negative Zahl 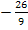geht und der Nenner gegen 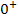. Wie kommt man denn nun aber auf das Ergebnis von 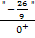? Minus durch Plus ergibt auf jeden Fall Minus. Das Vorzeichen des Endergebnisses muss Minus sein. Die Zahl 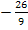geteilt durch eine Zahl, die fast Null ist, wird vom Betrag unendlich groß, weil eine Zahl, die fast Null ist, unendlich oft in die Zahl 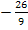hinein passt. Deshalb gilt: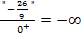

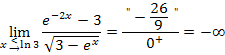
Die Gerade mit der Gleichung x = ln3 ist senkrechte Asymptote von .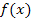

Weitere Asymptoten gibt es nicht. Damit ist die Aufgabe gelöst.

5. Bsp.:

Gegeben ist die Funktion 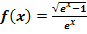. Ihr Graph wird mit 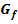bezeichnet.

a.) Ermittle die größtmögliche Definitionsmenge von 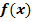und untersuche das Verhalten von 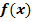für 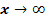! Gib auch die Gleichung der Asymptote vo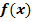n an!

b.) Berechne 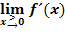und 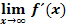! Was bedeuten diese beiden Grenzwerte geometrisch anschaulich für den Graph ?

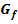Lösung:

Zu 5a.)

---