Grenzwerte von e- und ln-Funktionen

Waagrechte Asymptote:y = 0 (x-Achse)

Wegen 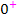nähert sich der Graph von 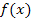im Unendlichen von oben an die x-Achse an.

Du schreibst in Prüfungen am besten Folgendes:

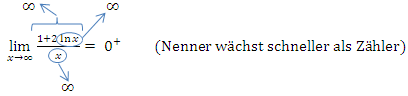
Damit du dir das Ganze besser vorstellen kannst, hier noch zusätzlich der Graph der Funktion. (Die Zeichnung war natürlich gar nicht verlangt.)

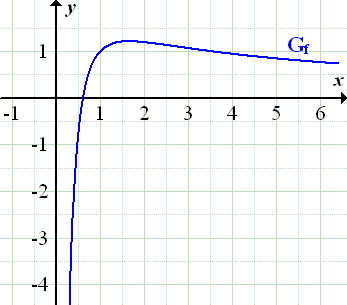
Abb.:Graph 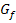der Funktion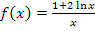

Man kann den Grenzwert 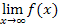aber auch folgendermaßen berechnen:

Alternative 1: Verwendung der bekannten Grenzwerte 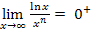und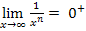

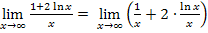
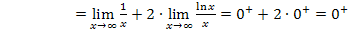
Alternative 2: Verwendung der Regel von L´Hospital

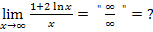
„Unendlich durch Unendlich“ ist ein unbestimmter Ausdruck. Um Grenzwerte zu berechnen, die auf unbestimmte Ausdrücke hinauslaufen, darf die Regel von L´Hospital verwendet werden. Wir leiten den Zähler und den Nenner getrennt ab und versuchen danach erneut den Grenzwert zu bestimmen.

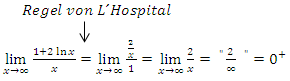
An den bisher gezeigten Beispielen dieses Teils konntest du sehen, wie typische Aufgaben zum Thema Grenzwerte bei e- und ln-Funktionen gelöst werden können. Die bisher besprochenen Grenzwerte aus den Beispielen 1 bis 6 solltest du auf jeden Fall selbständig lösen können. Mit einer ähnlichen Aufgabe wirst du vermutlich auch in deiner Abi-Prüfung konfrontiert werden und mit größter Wahrscheinlichkeit auch schon vorher in einer oder mehreren Schulaufgaben bzw. Stehgreifaufgaben.

Weitere Aufgabenbeispiele zum Thema „Grenzwerte von e- und ln-Funktionen“ findest du auch unter:Komplette Kurvendiskussion bei e- und ln-Funktionen und Funktionenscharen mit e- oder ln

Die nun folgenden Aufgabenbeispiele behandeln Grenzwerte, die zum Teil über das normale Niveau des Gymnasiums bzw. der Technik-FOS/BOS hinausgehen. Sie sind nur für Schüler interessant, die entweder vorhaben später ein Studium aus dem Bereich Mathematik oder Technik aufzunehmen, oder für Schüler, deren Lehrer im Schulunterricht ähnliche Grenzwerte wie 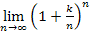tatsächlich besprochen hat. Einige wenige Lehrer führen die Eulersche Zahl e nämlich über den 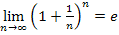ein. Deshalb soll auf dieser website auch darauf eingegangen werden.

Die Zahl e als Grenzwert

Es lässt sich zeigen, dass gilt:

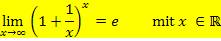
Dieser Grenzwert gilt tatsächlich für beliebige reelle Zahlen x. Der mathematische Beweis ist allerdings wirklich schwierig. Etwas einfacher wird es, wenn man für x nur natürliche, also ganze, positive Zahlen, d.h. Zahlen der Menge ℕzulässt. Wir beschränken uns daher auf  x ℕ. Um das deutlicher zu machen, schreiben wir an Stelle von x ab sofort n. (n für natürliche Zahl.) Funktionen mit der Definitionsmenge D = ℕ heißen übrigens Zahlenfolgen, kurz Folgen. Bei Folgen wird eine andere Schreibweise verwendet. Stat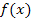t mit 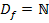schreibt man einfach 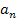oder .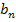

---