b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Dann jetzt die Antwort auf die Frage:
Der Punkt Q´liegt bei x = 1,5 auf der Ableitungsfunktion. Seine y-Koordinate ist y = -1. Somit hat die unbekannte Funktion  an der Stelle x = 1,5 die Steigung -1. Die y-Koordinate eines Punktes von
an der Stelle x = 1,5 die Steigung -1. Die y-Koordinate eines Punktes von  , also der Funktionswert der Ableitungsfunktion, gibt schließlich die Steigung von
, also der Funktionswert der Ableitungsfunktion, gibt schließlich die Steigung von  an dieser Stelle an.
an dieser Stelle an.
Merke:
Die y-Koordinate eines Punktes von 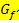 gibt die Steigung von
gibt die Steigung von 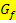 an der Stelle x an.
an der Stelle x an.
Jetzt aber zu der gesamten Funktion. Hier noch einmal der gegebene Graph der Ableitungsfunktion:
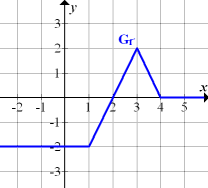
Man erkennt, dass der gezeigte Graph der Ableitungsfunktion aus mehreren Einzelstücken zusammengesetzt ist. Er besteht aus der waagrechten Gerade y = -2 für 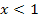 , einer steigenden Gerade für
, einer steigenden Gerade für 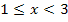 , einer fallenden Gerade für
, einer fallenden Gerade für 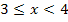 und einer zweiten waagrechten Gerade y = 0 für
und einer zweiten waagrechten Gerade y = 0 für 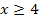 . (Streng genommen kann man eigentlich gar nicht sagen, wo das Gleichheitszeichen dazu genommen wird. Ob beispielsweise die Stelle x = 1 nun zu der waagrechten Gerade y = -2 oder zu der steigenden Gerade gezählt wird, ist reine Geschmackssache. An den Knickstellen x = 1, x = 3 und x = 4 muss man also selbst eine Entscheidung treffen, ob man den entsprechenden Punkt entweder zum linken oder rechten Teil des Graphen zählt. Hier wurde er immer zum rechten Teil gezählt. Dies ist reine Geschmackssache. Wichtig ist allerdings, dass die jeweiligen Punkte genau einem Teil zugerechnet werden.)
. (Streng genommen kann man eigentlich gar nicht sagen, wo das Gleichheitszeichen dazu genommen wird. Ob beispielsweise die Stelle x = 1 nun zu der waagrechten Gerade y = -2 oder zu der steigenden Gerade gezählt wird, ist reine Geschmackssache. An den Knickstellen x = 1, x = 3 und x = 4 muss man also selbst eine Entscheidung treffen, ob man den entsprechenden Punkt entweder zum linken oder rechten Teil des Graphen zählt. Hier wurde er immer zum rechten Teil gezählt. Dies ist reine Geschmackssache. Wichtig ist allerdings, dass die jeweiligen Punkte genau einem Teil zugerechnet werden.)
Wir werden im Folgenden versuchen, die Gleichung der Ableitungsfunktion  aufzustellen und daraus die Gleichung der Funktion
aufzustellen und daraus die Gleichung der Funktion  soweit möglich zu folgern. Da die Ableitungsfunktion aus mehreren einzelnen Stücken zusammengesetzt ist, muss auch die Funktion
soweit möglich zu folgern. Da die Ableitungsfunktion aus mehreren einzelnen Stücken zusammengesetzt ist, muss auch die Funktion  stückweise definiert sein, also aus mehreren Teilen zusammengesetzt sein. Daher gehen wir auch stückweise vor. Fangen wir ´mal mit dem Teil ganz links bei
stückweise definiert sein, also aus mehreren Teilen zusammengesetzt sein. Daher gehen wir auch stückweise vor. Fangen wir ´mal mit dem Teil ganz links bei  an. Hier verläuft
an. Hier verläuft  waagrecht, es gilt offensichtlich:
waagrecht, es gilt offensichtlich:
Für 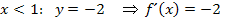
Die Ableitung ist hier also immer konstant gleich -2. Die Ableitung entspricht der Steigung der Funktion  . Deshalb können wir folgern, dass der Funktionsgraph
. Deshalb können wir folgern, dass der Funktionsgraph  für
für 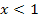 immer die Steigung -2 haben muss. Die y-Koordinate eines Punktes auf der Ableitungsfunktion entspricht schließlich der Steigung des Graphen der Funktion
immer die Steigung -2 haben muss. Die y-Koordinate eines Punktes auf der Ableitungsfunktion entspricht schließlich der Steigung des Graphen der Funktion  an dieser Stelle. Die y-Koordinate der Ableitungsfunktion ist in diesem Bereich immer gleich -2, daher muss die Funktion
an dieser Stelle. Die y-Koordinate der Ableitungsfunktion ist in diesem Bereich immer gleich -2, daher muss die Funktion  hier immer die Steigung -2 besitzen. Nur Geraden haben eine konstante Steigung, also eine Steigung, die sich nicht ändert. Es muss sich daher bei
hier immer die Steigung -2 besitzen. Nur Geraden haben eine konstante Steigung, also eine Steigung, die sich nicht ändert. Es muss sich daher bei  für
für 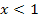 um eine Gerade mit der Steigung -2 handeln. Es gilt somit:
um eine Gerade mit der Steigung -2 handeln. Es gilt somit:

