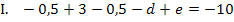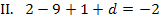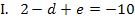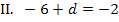Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Lösung:
In dieser Aufgabe ist die zweite Ableitung der gesuchten Funktion gegeben. Die zweite Ableitung lautet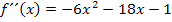 
. Da 
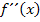eine quadratische Funktion ist, muss die erste Ableitung ein Polynom dritten Grades und die Funktion 
ein Polynom vierten Grades sein. Beim Ableiten nimmt schließlich die Potenz von x immer um jeweils Eins ab und umgekehrt beim Integrieren / „Hochleiten“ um Eins zu. (Vergleiche auch:Einfache Ableitungsregeln) Wir suchen also eine Polynomfunktion vierten Grades.
Dafür gibt es zwei verschiedene Lösungsmöglichkeiten. Die erste Methode kann von allen Schülern verwendet werden, dauert jedoch ein klein wenig länger. Die zweite Methode ist nur für Schüler geeignet, die bereits gelernt haben Polynome zu integrieren, also „hochzuleiten“.
1. Methode
Allgemeiner Ansatz für eine Polynomfunktion vierten Grades:
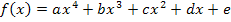
Wir bilden allgemein die ersten beiden Ableitungen:
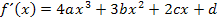
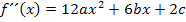
Laut Angabe soll die zweite Ableitung 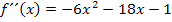sein. Mit Hilfe eines sogenannten Koeffizientenvergleichs lassen sich drei Gleichungen aufstellen.
Du weißt nicht, wie ein Koeffizientenvergleich funktioniert? Kein Problem! Das ist nicht schwer. 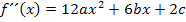und 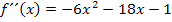muss logischerweise das Gleiche sein. Die Zahl, die bei 
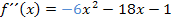vor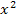 
steht, muss also das Gleiche sein wie der Ausdruck, der bei 
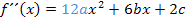vor 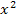steht. Deshalb gilt: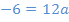 
Das gleiche Prinzip wendet man danach an bei der Zahl bzw. dem Ausdruck vor x, genauer gesagt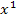 
, und dann auch noch bei der Zahl bzw. dem Ausdruck ganz ohne x, also bei 
.
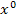Koeffizientenvergleich:
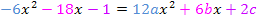
Aus dem Vergleich der Koeffizienten bei 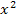ergibt sich: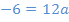
Aus dem Vergleich der Koeffizienten bei 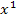ergibt sich: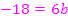 
Aus dem Vergleich der Koeffizienten bei 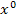ergibt sich: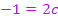 
Wir können diese Gleichungen leicht umstellen und so a, b und c berechnen.
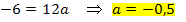
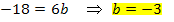
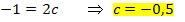
Wir setzten diese Wert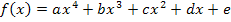e in ein.
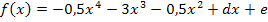
Die erste Ableitung lautet dann:
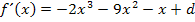
Nun müssen wir noch die letzten beiden Unbekannten d und e berechnen. Dazu brauchen wir die restlichen Angaben:
Der Graph enthält den Punkt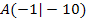 
, so dass gilt: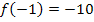 
Außerdem verläuft die Tangente im Punkt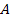 
parallel zur Gerade 
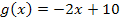. Da die Tangente parallel zu der Gerade 
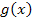ist, hat sie die gleiche Steigung. Die Gerade hat die Steigung 
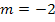und somit auch die Tangente im Punkt 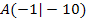. Das bedeutet, dass die gesuchte Funktion bei 
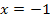die Steigung/erste Ableitung -2 besitzt. Das drückt 
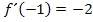aus.
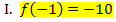
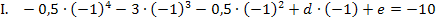
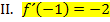
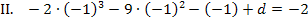
Wir vereinfachen die beiden Gleichungen, indem wir jeweils den vorderen Teil ausrechnen.
