Variante 3
1. Bsp.:
Berechne die Steigung der Tangente an die Funktion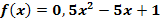 
im Punkt 
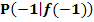mit Hilfe des Differenzialquotienten!
Lösung:
Gegeben: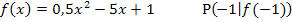 
Gesucht ist die Tangentensteigung im Punkt P, also die Ableitung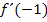 
. Sie soll mit dem Differenzialquotienten ermittelt werden.
Allgemeiner Ansatz für den Differenzialquotienten:
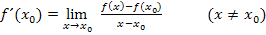
Der gegebene Punkt P hat die x-Koordinate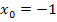 
. Das setzen wir in den allgemeinen Ansatz ein:
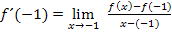
Mit der Funktionsgleichung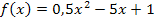 
ergibt sich:
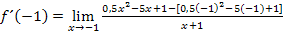
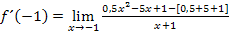
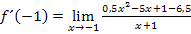
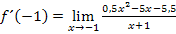
So, jetzt haben wir alles soweit möglich zusammengefasst. Aber wie kann nun der Grenzwert berechnet werden? Der Nenner würde ja gleich Null werden, wenn man in den vorliegenden Ausdruck für x den Wert -1 einsetzte. Der Ausdruck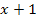 
muss erst aus dem Nenner verschwinden, bevor wir für x den Wert -1 einsetzten können. Momentan lässt sich 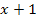allerdings noch nicht wegkürzen. Ausklammern lässt sich im Zähler leider auch nichts;eine binomische Formel lässt sich ebenfalls nicht anwenden. Also was tun?
Dieses Problem lässt sich auf zwei verschiedene Weisen lösen:Entweder man überführt den Zählerterm in seine vollständig faktorisierte Form (d.h. Produktform) oder man führt eine Polynomdivision durch. Damit du dir selbst aussuchen kannst, welche Methode dir besser liegt, werden im Folgenden beide Lösungswege vorgeführt.
1. Methode:Faktorisieren und danach Kürzen
Hinweis:Wenn du nicht mehr weißt, wie ein Term faktorisiert werden kann, siehe auch Faktorisierter Funktionsterm!
Wir müssen den Ausdruck, der sich im Zähler des Differenzialquotienten befindet, vollständig faktorisieren. Da sich in diesem Fall weder x ausklammern noch eine binomische Formel anwenden lässt, bleibt uns nur die folgende Methode:
· Gleich Null setzen:
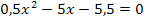
· Mitternachtsformel: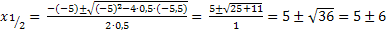 
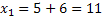
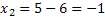
Da es zwei Lösungen gibt, gibt es auch zwei Linearfaktoren. Sie lauten in diesem Fall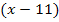 
und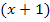 
. Hinter dem x in der Klammer steht jeweils eine der Lösungen aber mit umgedrehtem Vorzeichen.
· Faktorisierung:
Daher können wir den Differenzialquotienten nun auch in der faktorisierten Form schreiben:
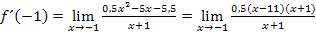
Du erkennst jetzt sicher sofort, dass man den Term x + 1 kürzen kann. Dadurch ergibt sich:
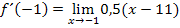
Nun kann der Grenzwert leicht berechnet werden. Man braucht nur noch für x den Wert -1 einsetzen. Das ist jetzt ja problemlos möglich;es gibt ja keinen Nenner mehr, der Null werden könnte.
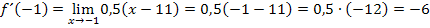
Die gesuchte Tangentensteigung der Funktion im Punkt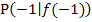 
ist daher – 6.
