Stetigkeit und Differenzierbarkeit
Merke:Immer zuerst überprüfen, ob die Funktion an der Stelle 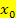 stetig ist, bevor du die Differenzierbarkeit an der Stelle
stetig ist, bevor du die Differenzierbarkeit an der Stelle 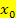 untersuchst!
untersuchst!
Ist die Funktion an der Stelle  gar nicht stetig, kann man sich die Untersuchung auf Differenzierbarkeit komplett schenken, weil die Funktion dann an der Stelle
gar nicht stetig, kann man sich die Untersuchung auf Differenzierbarkeit komplett schenken, weil die Funktion dann an der Stelle  sowieso nicht differenzierbar sein kann.
sowieso nicht differenzierbar sein kann.
nicht stetig bei 
 nicht differenzierbar bei
nicht differenzierbar bei 
Vorsicht:Die umgekehrte Aussage gilt nicht generell! Eine an der Stelle  nicht differenzierbare Funktion kann dort stetig sein oder auch nicht! Von der Aussage „nicht differenzierbar“ kann also nicht sofort auf die Stetigkeit bzw. Unstetigkeit geschlossen werden. Allerdings ist jede differenzierbare Funktion zwangsläufig stetig, da die Stetigkeit eine Voraussetzung für die Differenzierbarkeit ist.
nicht differenzierbare Funktion kann dort stetig sein oder auch nicht! Von der Aussage „nicht differenzierbar“ kann also nicht sofort auf die Stetigkeit bzw. Unstetigkeit geschlossen werden. Allerdings ist jede differenzierbare Funktion zwangsläufig stetig, da die Stetigkeit eine Voraussetzung für die Differenzierbarkeit ist.
differenzierbar bei 
![]()
 stetig bei
stetig bei 
Beispiele:
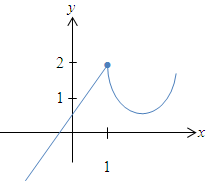 |
Die Funktion ist an der Stelle  stetig (keine Sprungstelle), aber nicht differenzierbar (Knick). stetig (keine Sprungstelle), aber nicht differenzierbar (Knick). |
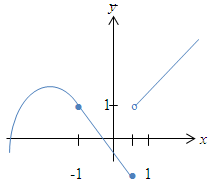 |
Die Funktion ist an der Stelle 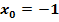 stetig (keine Sprungstelle) und differenzierbar (kein Knick), aber an der Stelle stetig (keine Sprungstelle) und differenzierbar (kein Knick), aber an der Stelle  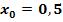 nicht stetig (Sprungstelle) und daher auch nicht differenzierbar. nicht stetig (Sprungstelle) und daher auch nicht differenzierbar. |
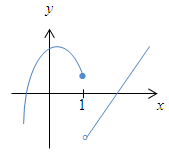 |
An der Stelle  ist die Funktion nicht stetig (Sprungstelle) und somit dort auch nicht differenzierbar. ist die Funktion nicht stetig (Sprungstelle) und somit dort auch nicht differenzierbar. |
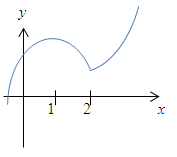 |
An der Stelle 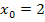 ist die Funktion zwar stetig, aber nicht differenzierbar (Knick). ist die Funktion zwar stetig, aber nicht differenzierbar (Knick). |
Eine Polynomfunktion (= ganzrationale Funktion) ist in 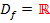 grundsätzlich stetig und differenzierbar;ihr Graph hat schließlich weder Sprungstellen noch Knicke. Anders sieht das bei Betragsfunktionen oder teilweise definierten Funktionenaus. Teilweise definierte Funktionen sind aus zwei oder mehr verschiedenen Teilfunktionen zusammengesetzte Funktionen:Die eine Funktionsgleichung gilt beispielsweise für
grundsätzlich stetig und differenzierbar;ihr Graph hat schließlich weder Sprungstellen noch Knicke. Anders sieht das bei Betragsfunktionen oder teilweise definierten Funktionenaus. Teilweise definierte Funktionen sind aus zwei oder mehr verschiedenen Teilfunktionen zusammengesetzte Funktionen:Die eine Funktionsgleichung gilt beispielsweise für 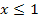 und die andere für
und die andere für 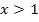 . Sie werden mit einer geschweiften Klammer geschrieben.
. Sie werden mit einer geschweiften Klammer geschrieben.
Beispiel für eine teilweise definierte Funktion:
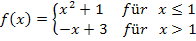
Die Funktion  setzt sich hier aus den beiden Teilfunktionen
setzt sich hier aus den beiden Teilfunktionen 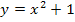 und
und 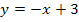 zusammen. Die Teilfunktion
zusammen. Die Teilfunktion 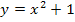 stellt eine nach oben geöffnete Normalparabel mit Scheitel bei
stellt eine nach oben geöffnete Normalparabel mit Scheitel bei 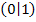 dar, die aber nur für
dar, die aber nur für 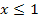 gilt.
gilt.

