Stetigkeit und Differenzierbarkeit

Oben gezeigte Definition der Stetigkeit noch einmal in Worten:Ist das Ergebnis des Limes der Funktion von rechts gleich dem des Limes von links und stimmt dieses Ergebnis auch mit dem Funktionswert an der Stelle 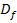überein, ist die Funktion an der Stelle stetig, d.h. sie hat dort keine Sprungstelle.

Anschaulich bedeutet das:Wenn man auf dem Graphen der Funktion 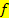mit dem rechten Zeigefinger von rechts und gleichzeitig mit dem linken Zeigefinger von links an die Stelle 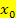herangeht, und es treffen sich die Fingerspitzen, dann ist die Funktion 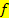an der Stelle 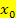stetig.

Man muss also den linksseitigen und den rechtsseitigen Limes von an der Stelle bilden, sowie den Funktionswert 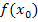. Sind alle Ergebnisse gleich, ist die Funktion an der Stelle stetig.

Sind zwar die beiden Grenzwerte gleich, die Funktion ist aber an der Stelle 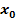nicht definiert, dann sagt man die Funktion ist „stetig ergänzbar“. Der Graph hat dann ein Loch an der Stelle . (Siehe auch stetig ergänzbare, stetig behebbare bzw. stetig fortsetzbare  Definitionslücke!) Die Funktion ist nicht definiert an der Stelle , wenn keine der Teilfunktionen an der Stelle definiert ist. Anders gesagt:Wenn bei beiden Teilfunktionen jeweils 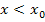bzw. 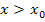steht, aber bei kein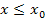er oder 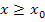, ist die Funktion nicht definiert an der Stelle , also wenn bei keiner der Teilfunktionen das Gleichheitszeichen dabei steht.

Die benötigten Grenzwerte kann man entweder einfach durch Einsetzen von in die beiden Teilfunktionen berechnen oder umständlicher mit der h-Methode. Wir schauen uns die Berechnung der Grenzwerte am besten gleich an unserem Einführungsbeispiel an.

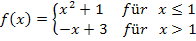
1. Methode:Grenzwerte berechnen durch Einsetzten von in beide Teilfunktionen

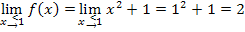
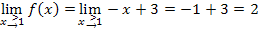
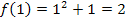
Alle drei Ergebnisse sind gleich, daher ist die Funktion an der Stelle stetig. Das bedeutet anschaulich:Die Funktion hat keine Sprungstelle;die Parabel stößt im Punkt 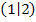direkt mit der Gerade zusammen.

Erläuterungen zur Berechnung der Grenzwerte bzw. des Funktionswertes:

Um den linksseitigen Grenzwert, also 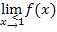in diesem Beispiel zu berechnen, muss die für 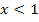geltende Teilfunktion, also 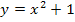verwendet werden. Das Ergebnis dieses Grenzwertes erhält man, indem man in die Parabelgleichung für x genau den Wert einsetzt.

Um den rechtsseitigen Grenzwert, also 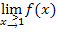zu berechnen, muss in diesem Beispiel die für 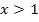geltende Teilfunktion 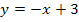verwendet werden. Das Ergebnis dieses Grenzwertes erhält man durch Einsetzen von in die Geradengleichung.

---