Die Quotientenregel
Um den Bruch selbst abzuleiten, benötigt man logischerweise die Quotientenregel, weil im Nenner x vorkommt. Aber Vorsicht:Der Zähler der Funktion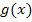 
enthält kein x. Im Beispiel 4c.) wurde schon auf diese Problematik hingewiesen. Die Quotientenregel beginnt bekanntlich mit u´, also mit der Ableitung des Zählers, welche in diesem Beispiel 0 ist. (Die Zahl 1 abgeleitet ist schließlich 0.) Keinesfalls darfst du diese 0 einfach weglassen und bloßden Nenner v hinschreiben! Würdest du das machen, würde der Nenner v im Zähler der Ableitung nämlich stehen bleiben, was definitiv falsch wäre. Korrekt ist es dagegen, bei der Quotientenregel mit 
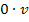zu beginnen oder den Ausdruck 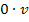komplett wegzulassen und gleich mit 
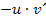zu beginnen. Das Ganze muss dann natürlich noch durch 
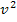dividiert werden, also durch den Nenner zum Quadrat. Falls dir das noch nicht ganz klar sein sollte, schaust du dir die im Folgenden gezeigte Lösung genau an. Danach sollte dir die Problematik klar sein, die sich dadurch ergibt, dass die Funktionsgleichung im Zähler kein x enthält. Wenn du es dir zutraust, kannst du natürlich gleich ´mal alleine versuchen 
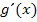zu bilden.
Zur Erinnerung: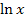 
abgeleitet ist 
.
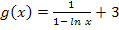
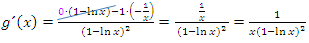
Wenn dir der letzte Umformungsschritt von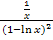 
zu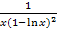 
nicht klar ist, siehe:Nähere Erklärungen zur folgenden Umformung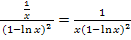 
Hättest du die 0 im Zähler bei der Quotientenregel weggelassen, hätte sich für die Ableitung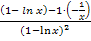 
ergeben;d.h. 
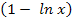wäre nicht weggefallen, was natürlich falsch gewesen wäre.
Also immer Vorsicht, wenn im Zähler eines Bruchs, den du mit der Quotientenregel ableiten musst, kein x vorkommt!
Wir haben die Ableitung gebildet und soweit möglich vereinfacht;somit ist die Aufgabe an sich gelöst.
Für interessierte Schüler:
An Hand der Ableitung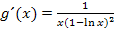 
lässt sich in diesem Fall ohne weitere Rechnung sofort einiges über den Verlauf des Graphen von 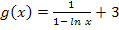aussagen.
Die Funktion 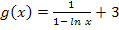ist nur für x 
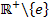definiert, da man bei 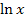nur positive Zahlen einsetzen kann und wegen 
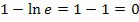der Nenner für 
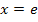Null ergeben würde. (Zur Erinnerung: 
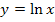ist ausschließlich für positive x definiert.) Deshalb stellt x hier eine positive Zahl (ungleich e) dar. Dadurch ist die Ableitung 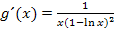immer positiv. Der Zähler ist ja offensichtlich positiv;der Nenner ist für x 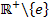ebenfalls positiv, da x bei dieser Definitionsmenge positiv ist und die Klammer wegen des Quadrats auch. Es gilt also: 
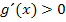Das bedeutet, dass der Funktionsgraph 
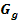streng monoton steigend ist und somit kein Extremum haben kann.
