1. Flächenberechnungenmit Hilfe von Integralen
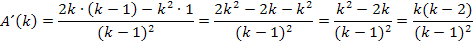
Berechnung des Extremums von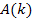 
:
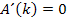
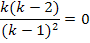
Ein Bruch ist gleich Null, wenn der Zähler gleich Null und der Nenner nicht gleich Null ist. Der Nenner wird für k >1 nicht gleich Null. Wir dürfen deshalb einfach den Zähler gleich Null setzen. (Wenn du einfach bei der Gleichung mit dem Nenner multiplizierst, kommst du auf das gleiche Ergebnis, denn die rechte Seite der Gleichung wird dabei gleich Null wegen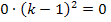 
.)
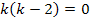
Jetzt bitte nicht ausmultiplizieren, das würde die Sache nur verkomplizieren. Du kannst die Lösungen der Gleichung sofort ablesen. Dazu musst du dir nur überlegen, für welche Werte von k die einzelnen Faktoren des vorliegenden Produkts Null ergeben. Ein Produkt ist schließlich gleich Null, wenn einer der Faktoren gleich Null ist. So ergeben sich die folgenden beiden Lösungen:
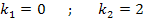
Wegen k >1 gilt nur die zweite Lösung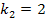 
.
Nun wissen wir, dass sich nur für k = 2 ein Extremum von 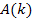ergeben kann. Dass es sich wirklich um ein Extremum und nicht etwa um einen Terrassenpunkt handelt, müssen wir noch zeigen. Das könnten wir entweder mit Hilfe der Zweiten Ableitung f ´´(x) machen oder mit der Untersuchung des Monotonieverhaltens von 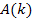. Die zweite Ableitung lässt sich nur mit großem Rechenaufwand ermitteln, daher untersuchen wir lieber die Monotonie. Das geht hier wesentlich schneller.
Beachte, dass hier k >1 gilt! Nur in diesem Bereich muss die Monotonie untersucht werden. Dazu müssen wir das Vorzeichen der Ableitung bestimmen.
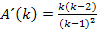
Der Nenner der Ableitung ist wegen der geraden Potenz sowieso positiv. Nur der Zähler kann sein Vorzeichen ändern. Wegen k >1 ist der Faktor k ebenfalls positiv;wir brauchen nur den Faktor (k – 2) betrachten.
| k |  |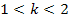
 |
 |
 |
 |
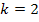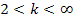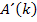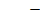0 |  + |
 |
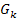streng monoton fallend | TIP | streng monoton steigend |
 |
 |
Für k = 2 liegt ein Minimum von 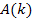vor. Es handelt sich um ein absolutes Minimum, da sich die Monotonie nur an der Stelle k = 2 ändert. (Gibt es nur eine Stelle, wo sich die Monotonie ändert, handelt es sich immer um ein absolutes Extremum, also um einen Punkt des Graphen, der am absolut höchsten bzw. tiefsten liegt.)
Jetzt fehlt nur noch der minimale Flächeninhalt. Wir erhalten ihn durch das Einsetzen des soeben ermittelten Wertes k = 2 in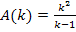 
.
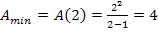
Für k = 2 ergibt sich der kleinstmögliche Flächeninhalt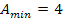 
FE.
| Wichtige Hinweise:
Wenn du Schwierigkeiten hattest, dir vorweg den Verlauf der Graphen Betrachte besser die Schar im Ganzen, so wie wir das oben gemacht haben, also ohne eine konkrete Zahl einzusetzen. Wenn du dir den Verlauf der Graphen Besser ist es, sich vorher zu überlegen, ob der Betrag überhaupt nötig ist, und falls die Fläche oberhalb der x-Achse liegt, ohne Betrag zu rechnen, so wie das oben vorgeführt wurde. Wenn du eine Fläche, die definitiv unterhalb der x-Achse liegt, in Abhängigkeit von einem Scharparameter berechnen musst, schreibst du an Stelle des Betrages besser ein Minuszeichen vor das Integral (oder du integrierst stattdessen ausnahmsweise in umgekehrter Richtung, also von der größeren zur kleineren Grenze). Vorsicht, wenn bei den Grenzen ein Scharparameter vorkommt! Achte dabei besonders darauf, dass du wirklich von der kleineren zur größeren Grenze integrierst. Nur dann ist das Integral positiv, wenn die Fläche oberhalb der x-Achse liegt. Liegen die Nullstellen beispielsweise bei |
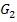bzw.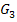 
mit Hilfe einer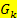 
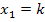und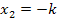 
, kann man nur für positive Werte von k davon ausgehen, dass –k die kleinere und k die größere Nullstelle ist. Nur für k >0 ist –k die untere Grenze und k die obere Grenze des Integrals. Für k < 0 wäre es dagegen genau umgekehrt! Für negative Werte von k ist nämlich –k eine positive Zahl und k eine negative Zahl. Deshalb ist dann –k größer als k und man müsste von k (untere Grenze) bis –k (obere Grenze) integrieren.
