3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Deshalb gilt:
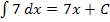 und
und 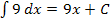
Integriert man eine Konstante, d.h. eine feste Zahl nach dx, kommt einfach ein x dazu. Weil 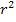 in unserem Fall ebenfalls eine Konstante ist, kommt bei der Integration von
in unserem Fall ebenfalls eine Konstante ist, kommt bei der Integration von 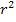 nach dx ebenso ein x dazu und es gilt:
nach dx ebenso ein x dazu und es gilt: 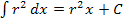
Weil es sich bei 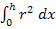 um ein bestimmtes Integral (Integral mit Grenzen) handelt, können wir auf „+ C“ verzichten. Nun ist dir hoffentlich klar, warum gilt:
um ein bestimmtes Integral (Integral mit Grenzen) handelt, können wir auf „+ C“ verzichten. Nun ist dir hoffentlich klar, warum gilt: 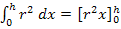
Solltest du Probleme bei der Berechnung des Integrals gehabt haben, wäre es gut, wenn du den Teil Die Stammfunktion F(x) und einfache Integrationsregeln wiederholen würdest.
Zu 5b.)
Herleitung der Kegelformel: 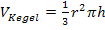
Zuerst brauchen wir eine geeignete Funktion 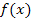 , die bei Rotation um die x-Achse einen Kegel mit Radius r und der Höhe h ergibt. Wir nehmen eine schräge Gerade, welche durch den Ursprung des Koordinatensystems und durch den Punkt P(h;r) verläuft, und lassen sie um die x-Achse rotieren. Siehe Skizze!
, die bei Rotation um die x-Achse einen Kegel mit Radius r und der Höhe h ergibt. Wir nehmen eine schräge Gerade, welche durch den Ursprung des Koordinatensystems und durch den Punkt P(h;r) verläuft, und lassen sie um die x-Achse rotieren. Siehe Skizze!
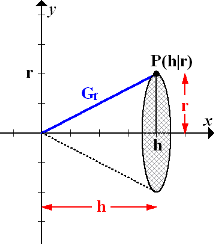
Abb.:Der Graph  rotiert um die x-Achse. Dadurch entsteht ein Kegel mit der Höhe h und dem Radius r.
rotiert um die x-Achse. Dadurch entsteht ein Kegel mit der Höhe h und dem Radius r.
Nun müssen wir die Gleichung der Geraden 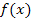 aufstellen. Sie verläuft durch den Ursprung des Koordinatensystems und den Punkt P(h| r). Wir gehen von der allgemeinen Geradengleichung y = mx + t aus. Da die Gerade durch den Ursprung verläuft, ist der y-Achsenabschnitt t = 0. Die Steigung m kannst du entweder direkt aus der Zeichnung ablesen oder mit der Formel
aufstellen. Sie verläuft durch den Ursprung des Koordinatensystems und den Punkt P(h| r). Wir gehen von der allgemeinen Geradengleichung y = mx + t aus. Da die Gerade durch den Ursprung verläuft, ist der y-Achsenabschnitt t = 0. Die Steigung m kannst du entweder direkt aus der Zeichnung ablesen oder mit der Formel 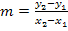 berechnen. Dabei sind die Punkte
berechnen. Dabei sind die Punkte 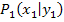 und
und 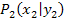 zwei beliebige Geradenpunkte. Sagen wir mal, dass hier der Punkte
zwei beliebige Geradenpunkte. Sagen wir mal, dass hier der Punkte 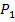 dem Ursprung (0|0) und der Punkte
dem Ursprung (0|0) und der Punkte 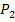 unserem Punkt P(h| r) entspricht. Dann ergibt die Formel für die Steigung:
unserem Punkt P(h| r) entspricht. Dann ergibt die Formel für die Steigung:
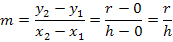
Einsetzen von 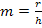 und t = 0 in die allgemeine Geradengleichung y = mx + t liefert:
und t = 0 in die allgemeine Geradengleichung y = mx + t liefert:
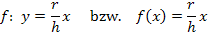
Damit sich nur das Teilstück der Geraden von 0 bis h ergibt, wählen wir wie schon in Teilaufgabe 5a.) die Definitionsmenge 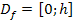 .
.
Da der Kegel durch Rotation von  um die x-Achse entsteht, können wir das Kegelvolumen mit der Formel
um die x-Achse entsteht, können wir das Kegelvolumen mit der Formel 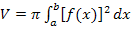 berechnen.
berechnen.
Mit 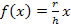 und a = 0 und b = h ergibt sich:
und a = 0 und b = h ergibt sich:
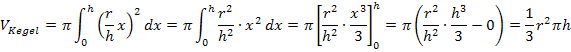
Damit haben wir die Formel für das Volumen eines Kegels mit Radius r und Höhe h hergeleitet.
3.2 Rotation um die y-Achse
Bisher haben wir uns ausschließlich mit der Volumenberechnung von Rotationskörpern beschäftigt, die durch Rotation eines Funktionsgraphen  um die x-Achse entstanden. Wie berechnet man nun aber das Volumen eines Rotationskörpers, der durch Rotation eines Funktionsgraphen
um die x-Achse entstanden. Wie berechnet man nun aber das Volumen eines Rotationskörpers, der durch Rotation eines Funktionsgraphen  um die y-Achse entsteht? Dafür stehen uns zwei verschiedene Rechenwege zur Verfügung.
um die y-Achse entsteht? Dafür stehen uns zwei verschiedene Rechenwege zur Verfügung.
Volumen eines Rotationskörpers, der durch Rotation von 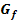 um die y-Achse entsteht um die y-Achse entsteht
1. Methode:
Grundprinzip: Wir kennen die Formel für das Volumen eines Rotationskörpers, der durch Rotation des Graphen einer Funktion Bei der Rotation um die y-Achse geht man entsprechend vor, nur dass dabei an Stelle von So ergibt sich die Formel für die Rotation um die y-Achse: Damit es bei der Rotation von
Anleitung: · Löse die Funktion Die nach x aufgelöste Form der Funktion wird mit · Berechne das Volumen mit der Formel: Hinweis: Die Integrationsgrenzen y = a und y = b sind waagrecht verlaufende Geraden. Bei dieser Methode wird schließlich nach dy und nicht nach dx integriert! Der Graph Herleitung der Formel (Grundgedanke): Die gezeigte Formel ließe sich herleiten, indem man sich den Rotationskörper in unendlich viele, senkrecht übereinander liegende Scheibchen von unendlich kleiner Höhe |
Hier ein konkretes Beispiel zur Rotation eines Funktionsgraphen um die y-Achse.

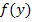 gearbeitet wird und statt nach dx nun nach dy integriert werden muss. Wir gehen also von der Formel für die Rotation um die x-Achse aus und ersetzen rein formal einfach x durch y.
gearbeitet wird und statt nach dx nun nach dy integriert werden muss. Wir gehen also von der Formel für die Rotation um die x-Achse aus und ersetzen rein formal einfach x durch y.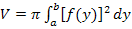
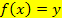
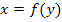
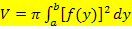
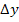 zerteilt denkt. Macht man die Höhe der Scheibchen
zerteilt denkt. Macht man die Höhe der Scheibchen 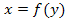 Durch Summieren der Einzelvolumina dieser unendlich vielen Zylinder mit unendlich kleiner Höhe
Durch Summieren der Einzelvolumina dieser unendlich vielen Zylinder mit unendlich kleiner Höhe 