3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Beim Integrieren nach dy muss man sich dann logischerweise auf die y-Potenzen konzentrieren.
Der Sektkelch hat somit ein Volumen von 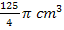 , also ungefähr
, also ungefähr 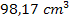 . Das sind umgerechnet ungefähr 0,098 Liter oder 98 ml, d.h. knapp 100 ml.
. Das sind umgerechnet ungefähr 0,098 Liter oder 98 ml, d.h. knapp 100 ml.
Wenn dir das Integrieren nach dy nicht liegt, kannst du stattdessen die 2. Methode anwenden. Dabei musst du vorher die Umkehrfunktion 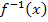 der Funktion
der Funktion 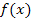 bilden, kannst dann aber ganz normal nach dx integrieren. Für welche Methode du dich entscheidest, bleibt dir überlassen. Das ist reine Geschmackssache. Schau dir auch die 2. Methode an und probiere sie einmal selbst aus, bevor du dich dann für eine der beiden Methoden entscheidest. Es reicht völlig, wenn du eine der beiden Methoden beherrscht.
bilden, kannst dann aber ganz normal nach dx integrieren. Für welche Methode du dich entscheidest, bleibt dir überlassen. Das ist reine Geschmackssache. Schau dir auch die 2. Methode an und probiere sie einmal selbst aus, bevor du dich dann für eine der beiden Methoden entscheidest. Es reicht völlig, wenn du eine der beiden Methoden beherrscht.
Volumen eines Rotationskörpers, der durch Rotation von 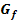 um die y-Achse entsteht um die y-Achse entsteht
2. Methode:
Grundprinzip: Wir betrachten statt des Rotationskörpers, der durch die Rotation des Graphen  um die y-Achse entsteht, denjenigen Rotationskörper, der durch Rotation des Graphen der Umkehrfunktion um die y-Achse entsteht, denjenigen Rotationskörper, der durch Rotation des Graphen der Umkehrfunktion 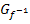 um die x-Achse entsteht. Dieser Rotationskörper hat das gleiche Volumen wie der ursprüngliche Rotationskörper, der durch die Rotation des Graphen um die x-Achse entsteht. Dieser Rotationskörper hat das gleiche Volumen wie der ursprüngliche Rotationskörper, der durch die Rotation des Graphen  um die y-Achse entstand. um die y-Achse entstand.
Der Graph der Umkehrfunktion 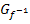 ergibt sich bekanntlich durch Spiegelung des Graphen ergibt sich bekanntlich durch Spiegelung des Graphen  an der Winkelhalbierenden y = x. Die Umkehrfunktion lassen wir nun um die x-Achse rotieren. Dann kann mit der bekannten Formel an der Winkelhalbierenden y = x. Die Umkehrfunktion lassen wir nun um die x-Achse rotieren. Dann kann mit der bekannten Formel 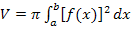 für die Rotation um die x-Achse gearbeitet werden. Man muss dabei anstatt für die Rotation um die x-Achse gearbeitet werden. Man muss dabei anstatt 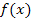 natürlich natürlich 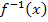 verwenden. Es ist schließlich der Graph der Umkehrfunktion verwenden. Es ist schließlich der Graph der Umkehrfunktion 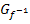 , der um die x-Achse rotiert. , der um die x-Achse rotiert.
So kommt man auf die Formel für das Volumen eines Rotationskörpers bei Rotation von  um die y-Achse: um die y-Achse: 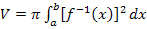
Anleitung:
· Ermittle die Umkehrfunktion 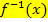 der Funktion der Funktion 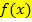 . Dazu kannst du entweder zuerst x gegen y vertauschen und dann nach y auflösen, oder umgekehrt zuerst nach x auflösen und danach x gegen y vertauschen. . Dazu kannst du entweder zuerst x gegen y vertauschen und dann nach y auflösen, oder umgekehrt zuerst nach x auflösen und danach x gegen y vertauschen.
(Den Graph der Umkehrfunktion 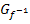 erhält man durch Spiegelung des Graphen erhält man durch Spiegelung des Graphen  an der Winkelhalbierenden y = x. Den Graph an der Winkelhalbierenden y = x. Den Graph 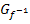 lässt man dann in Gedanken um die x-Achse rotieren.) lässt man dann in Gedanken um die x-Achse rotieren.)
· Berechne das Volumen mit der Formel: 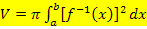
Hinweis: Die Integrationsgrenzen 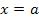 und und 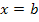 sind senkrecht verlaufende Geraden. Bei dieser Methode wird ganz normal nach dx integriert. Man lässt schließlich den Graph der Umkehrfunktion sind senkrecht verlaufende Geraden. Bei dieser Methode wird ganz normal nach dx integriert. Man lässt schließlich den Graph der Umkehrfunktion 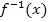 um die x-Achse rotieren. Auf die Werte a und b kommt man, indem man die Werte a und b von den waagrechten Geraden y = a und y = b nimmt, welche den Graph der Funktion um die x-Achse rotieren. Auf die Werte a und b kommt man, indem man die Werte a und b von den waagrechten Geraden y = a und y = b nimmt, welche den Graph der Funktion 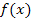 oben bzw. unten begrenzen. Wenn oben bzw. unten begrenzen. Wenn  streng monoton ist, sind dies die y-Koordinaten der Randpunkte der Funktion streng monoton ist, sind dies die y-Koordinaten der Randpunkte der Funktion 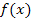 . Die Integrationsgrenzen ergeben sich also aus der Wertemenge . Die Integrationsgrenzen ergeben sich also aus der Wertemenge 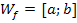 , was wiederum der Definitionsmenge , was wiederum der Definitionsmenge 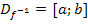 der Umkehrfunktion entspricht. der Umkehrfunktion entspricht. |
Wir berechnen das Volumen des Sektkelchs aus dem 1. Bsp. ein zweites Mal, nun aber nach der 2. Methode.
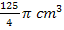 , also ungefähr
, also ungefähr 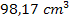 . Das sind umgerechnet ungefähr 0,098 Liter oder 98 ml, d.h. knapp 100 ml.
. Das sind umgerechnet ungefähr 0,098 Liter oder 98 ml, d.h. knapp 100 ml.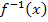 der Funktion
der Funktion 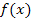 bilden, kannst dann aber ganz normal nach dx integrieren. Für welche Methode du dich entscheidest, bleibt dir überlassen. Das ist reine Geschmackssache. Schau dir auch die 2. Methode an und probiere sie einmal selbst aus, bevor du dich dann für eine der beiden Methoden entscheidest. Es reicht völlig, wenn du eine der beiden Methoden beherrscht.
bilden, kannst dann aber ganz normal nach dx integrieren. Für welche Methode du dich entscheidest, bleibt dir überlassen. Das ist reine Geschmackssache. Schau dir auch die 2. Methode an und probiere sie einmal selbst aus, bevor du dich dann für eine der beiden Methoden entscheidest. Es reicht völlig, wenn du eine der beiden Methoden beherrscht.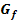 um die y-Achse entsteht
um die y-Achse entsteht

 um die y-Achse entsteht, denjenigen Rotationskörper, der durch Rotation des Graphen der
um die y-Achse entsteht, denjenigen Rotationskörper, der durch Rotation des Graphen der 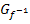 um die
um die 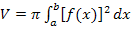 für die Rotation um die
für die Rotation um die 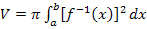
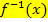
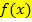
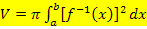
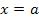 und
und 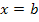 sind senkrecht verlaufende Geraden. Bei dieser Methode wird ganz normal nach dx integriert. Man lässt schließlich den Graph der Umkehrfunktion
sind senkrecht verlaufende Geraden. Bei dieser Methode wird ganz normal nach dx integriert. Man lässt schließlich den Graph der Umkehrfunktion 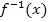 um die x-Achse rotieren. Auf die Werte a und b kommt man, indem man die Werte a und b von den waagrechten Geraden y = a und y = b nimmt, welche den Graph der Funktion
um die x-Achse rotieren. Auf die Werte a und b kommt man, indem man die Werte a und b von den waagrechten Geraden y = a und y = b nimmt, welche den Graph der Funktion 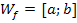 , was wiederum der Definitionsmenge
, was wiederum der Definitionsmenge 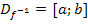 der Umkehrfunktion entspricht.
der Umkehrfunktion entspricht.