3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
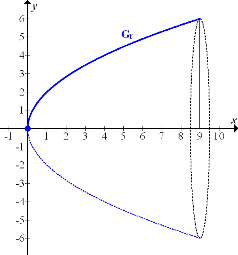
Abb.:Der Graph der Funktion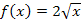 
mit 
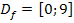rotiert um die x-Achse.
Nun zur Berechnung des Volumens des Rotationskörpers:
Wir setzen einfach in die folgende Formel ein und berechnen das entstehende Integral: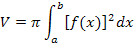 
Die Integrationsgrenzen sind durch die Definitionsmenge 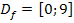festgelegt.
Es gilt:a = 0 und b = 9
Mit 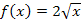ergibt sich:
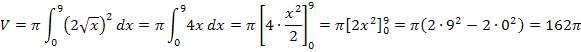
2. Bsp.:
Der Graph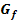 
rotiert um die x-Achse. Skizziere 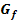und den zugehörigen Rotationskörper in einem Koordinatensystem. Berechne sodann das Volumen des Rotationskörpers mittels Integralrechnung und kontrolliere dein Ergebnis mit bekannten Volumenformeln.
a.)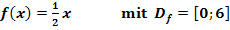 
b.)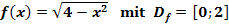 
Lösung:
Zu 2a.)
Die Funktion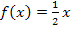 
ist eine lineare Funktion, da sie eine Funktion der Form 
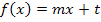ist. Wegen t = 0 verläuft die Gerade durch den Ursprung;ihre Steigung ist 
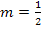. Um die Gerade zu zeichnen, braucht man also nur vom Ursprung 2 nach rechts und 1 nach oben zu gehen. (Steigungsdreieck) So erhältst du zusätzlich zum Ursprung einen weiteren Geradenpunkt. Damit kannst du 
leicht zeichnen. (Genauere Erklärungen bei:Geraden zeichnen) Laut Angabe gilt: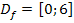 
Du darfst daher nur das Stück der Gerade zeichnen, das von x = 0 bis x = 6 geht.
Dieses Geradenstück lassen wir nun in Gedanken um die x-Achse rotieren. Skizzieren kannst du den entsprechenden Rotationskörper am besten, indem du das Geradenstück zuerst einmal an der x-Achse spiegelst und dann die Endpunkte auf der rechten Seite durch eine schmale Ellipse miteinander verbindest. Probiere das gleich mal alleine!
Deine Zeichnung müsste vom Prinzip her aussehen, wie die folgende Abbildung.
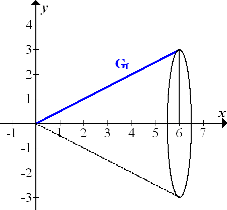
Abb.:Der Graph der Funktion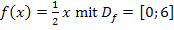 
rotiert um die x-Achse
Nun erkennt man, dass es sich bei dem vorliegenden Rotationskörper um einen (liegenden) Kegel handelt. Er hat die Höhe h = 6 und den Radius r = 3. (Der Radius r ergibt sich aus der y-Koordinate des rechten Endpunktes der Geraden 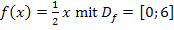. Man muss also nur für x die Zahl 6 in die Funktionsgleichung einsetzen, um den Radius des Kegels zu erhalten: 
)
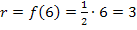Volumenberechnung des Rotationskörpers:
Zuerst berechnen wir das gesuchte Volumen mit Hilfe der Integralrechnung. Wir verwenden die folgende Formel:
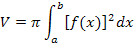
Die Integrationsgrenzen sind durch die Definitionsmenge 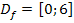festgelegt.
Es gilt:a = 0 und b = 6
Mit 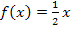ergibt sich:
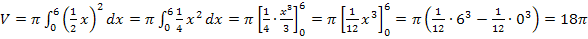
Nun überprüfen wir das Ergebnis, indem wir das Volumen V mit Hilfe der Formel für das Volumen eines Kegels berechnen.
Zur Erinnerung:
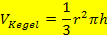
(Diese Formel findest du auch in deiner Formelsammlung bzw.
