Das bestimmte und das unbestimmte Integral
Aber Vorsicht:Du darfst dabei keinesfalls die additive Konstante „ + C “ vergessen, die man schließlich beim Integrieren nicht ermitteln kann. Weil wir zweimal nacheinander integrieren, müssen wir auch zwei verschiedene Bezeichnungen für die beiden Konstanten verwenden. Man könnte beispielsweise einmal „+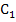 
“ bei der ersten Integration und einmal „+ 
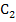“ bei der zweiten Integration schreiben.
Die zweite Ableitung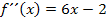 
ist hier ein Polynom 1. Grades, weil bei 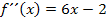die höchste x-Potenz x, also 
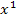ist. (Der Grad eines Polynoms ist immer die höchste Potenz der Variablen.) Wenn man 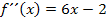zweimal nacheinander integriert, wird sich der Grad des Polynoms, also die höchste Potenz von x jeweils um 1, also insgesamt um 2 erhöhen. Die gesuchte Funktion muss daher ein Polynom dritten Grades sein, d.h. als höchste Potenz 
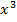haben. Die allgemeine Schreibweise einer Polynomfunktion dritten Grades ist:
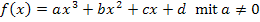
Die beiden hinteren Koeffizienten (Buchstabe vor x bzw. Buchstabe ohne x) sind dabei mit c und d bezeichnet. Genau diese Koeffizienten lassen sich nicht direkt durch die zweimalige Integration von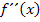 
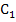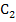ermitteln und wir müssen sie nachher gesondert berechnen. Deshalb verwenden wir für die Integrationskonstanten in dieser Aufgabe an Stelle von und lieber c und d.
1. Integration, um von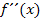 
auf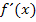 
zukommen
Hier noch einmal die angegebene zweite Ableitung: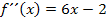
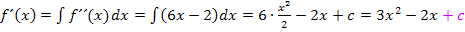
2. Integration, um von 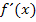auf 
zukommen
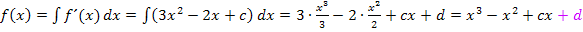
3. Berechnung von c und d
Um zwei Unbekannte zu berechnen, benötigt man zwei Gleichungen. Um diese beiden Gleichungen aufstellen zu können, braucht man zwei weitere Informationen. Diese sind versteckt in der Angabe, dass die Funktion das Extremum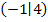 
hat. Wenn du dich fragst, wo denn hier zwei Informationen zu finden sind, dann überlege dir Folgendes:Es ist erstens der Kurvenpunkt 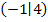angegeben, und zweitens die Tangentensteigung in diesem Punkt, denn die Steigung der Tangente muss bei einem Extremum gleich Null sein. (Die Tangente an 
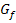im Extremum muss schließlich waagrecht verlaufen.) So kommt man zu den folgenden beiden Informationen:
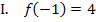
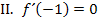
Hier noch einmal der allgemeine Ansatz für und :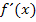
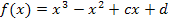
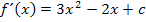
Aus den allgemeinen Ansätzen und mit den beiden Informationen I. und II. ergeben sich die folgenden Gleichungen:
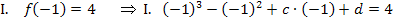
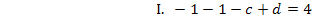
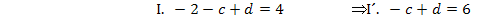
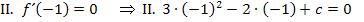
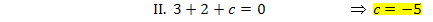
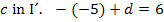
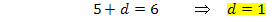
Nun müssen wir nur noch die berechneten Werte für c und d in 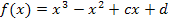einsetzen. Die gesuchte Funktionsgleichung lautet:
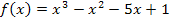
Fertig!
