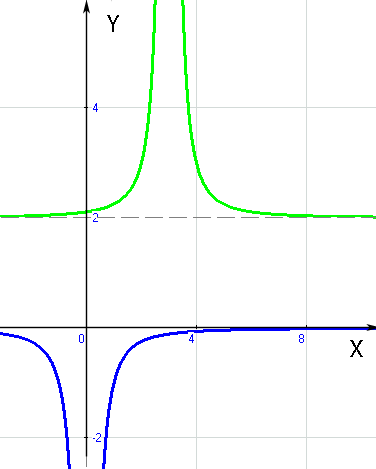
Graphisches Lösungsverfahren von Bruchgleichungen

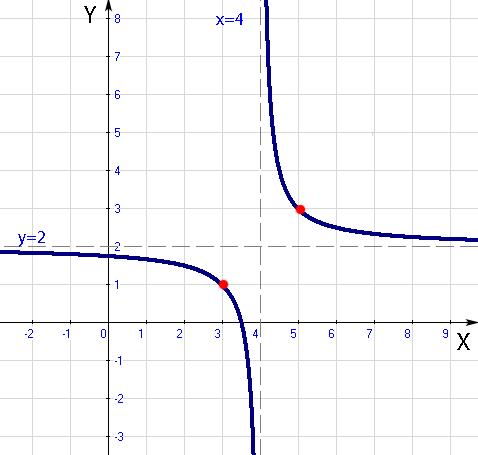
Jetzt kannst du sicher den Graph von f(x) in das Koordinatensystem einzeichnen, in das du bereits die Gerade g(x) gezeichnet hast. Du erkennst, dass sich zwei Schnittpunkte der beiden Graphen ergeben. Dann kannst du die x-Koordinaten der Schnittpunkte der beiden Funktionen ablesen. Das sind die gesuchten Lösungen unserer Bruchgleichung. Diese Bruchgleichung hat also zwei Lösungen.

Deine Zeichnung sollte im Prinzip aussehen wie die folgende Abbildung.

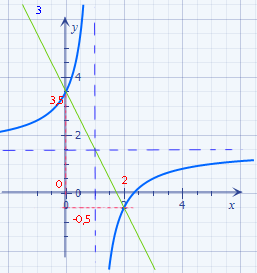
Abb.:Graph der Funktion f(x) = und der Funktion g(x) = mit ihren Schnittpunkten und 2|-0,5)

Aus der Zeichnung können die x-Koordinaten der Schnittpunkte x = 0 und x = 2 gut abgelesen werden. Die Lösungen der Bruchgleichung sind x = 0 und x = 2.

Wir machen für jede der beiden Lösungen noch die Probe.

Hier noch einmal die Gleichung:

Probe für x = 0:

(wahr)

Probe für x = 2:

(wahr)

Die Probe bestätigt:x = 0 und x = 2 sind tatsächlich die Lösungen der Bruchgleichung .

Bisher haben wir nur Bruchgleichungen behandelt, die entweder eine oder sogar zwei Lösungen hatten. Es gibt aber auch Bruchgleichungen, die gar keine Lösung besitzen. Schneiden sich die beiden Funktionsgraphen nicht, existiert auch keine Lösung der Gleichung, die durch das Gleichsetzen der Funktionsgleichungen entstanden ist. In den nächsten Beispielen wollen wir uns mit der Anzahl der Lösungen einer Bruchgleichung beschäftigen. Natürlich immer noch auf graphischem Weg! In diesem Beispiel sind ein paar kleine Gemeinheiten versteckt. Also Vorsicht, wenn du es alleine versuchst.

4. Bsp.:

Ermittle an Hand einer Übersichtsskizze die Anzahl der Lösungen der folgenden Bruchgleichungen!

a.)

b.)

c.)

Lösung:

zu 4a.)

Hier noch einmal die gegebene Bruchgleichung:

Wir wenden wieder das oben beschriebene graphische Lösungsverfahren an. Wir betrachten also die beiden Seiten der Gleichung jeweils als einzelne Funktionen.

Die linke Seite der Gleichung führt zur Funktion f(x) = . Das ist eine gebrochenrationale Funktion, da x im Nenner vorkommt. Ihr Graph ist daher eine Hyperbel. Die Gleichungen der Asymptoten lassen sich gut ablesen, da die Funktion in der Form f(x) = vorliegt.

f(x) =

Senkrechte Asymptote: x = 3

Waagrechte Asymptote: y = 2

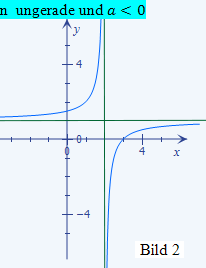
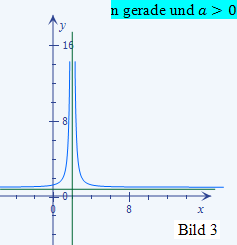
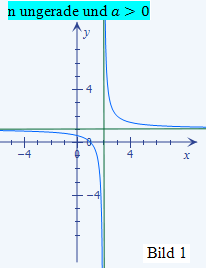
Das Vorzeichen von a ist positiv und die Potenz n des Nenners ist gerade. Daher ähnelt der Verlauf des Graphen von f(x) dem in Bild 3 (aus Bsp. 1) gezeigten Graphen.

Nachdem du ein paar Funktionswerte von f(x) berechnet hast, kannst du den Graph von f(x) leicht zeichnen.

So sollte dein Graph der Funktion aussehen

Die rechte Seite der Gleichung führt uns ebenfalls zu einer gebrochenrationalen Funktion, nämlich zu h(x) . Der Graph der Funktion h(x) ist eine Hyperbel mit der y-Achse als senkrechte Asymptote und der x-Achse als waagrechte Asymptote.

h(x)

Senkrechte Asymptote: x = 0 (y-Achse)

Waagrechte Asymptote: y = 0 (x-Achse)

Das Vorzeichen von a ist negativ und die Potenz n des Nenners ist gerade. Daher ähnelt der Verlauf des Graphen von f(x) dem in Bild 4 (aus Bsp. 1) gezeigten Graphen. Damit es hier nicht zu Missverständnissen kommt:Die Asymptoten von h(x) liegen natürlich auf den Koordinatenachsen;nur der qualitative Verlauf des Graphen von h(x) ist ähnlich zu Bild 4(aus Bsp. 1).

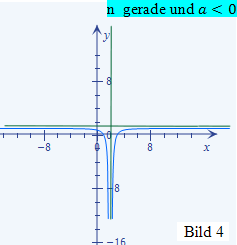
(aus Bsp. 1)

Jetzt rechnest du einfach noch ein paar Funktionswerte von h(x) aus und zeichnest den Graph von h(x) in das Koordinatensystem ein, in das du vorher schon die andere Hyperbel gezeichnet hast.

Deine Zeichnung sollte dann aussehen wie die folgende Abbildung.

Du erkennst sicher gleich, dass sich die beiden Graphen gar nicht schneiden können. Die gegebene Bruchgleichung hat keine Lösung.

Das hätte man eigentlich auch an einer groben Skizze erkennen können, ganz ohne irgendwelche Funktionswerte zu berechnen. Doch fällt es den meisten Schülern zu Beginn noch schwer gebrochenrationale Funktionen ganz ohne Funktionswerte zu zeichnen. Wenn es dir genauso geht, rechnest du doch besser noch einige Funktionswerte aus, bevor du den Graph zeichnest. Dass man auch ohne Funktionswerte nur an der Funktionsgleichung erkennt, wie der Graph ungefähr aussehen wird, ist einfach nur Erfahrungssache. Und die Erfahrung kommt einfach beim Üben.

zu 4b.)

Hier noch einmal die Angabe:

Lösung:

Hier müssen wir die beiden Funktionen f(x) = und h(x) = zeichnen oder zumindest grob skizzieren. Beide Funktionen liegen hier nicht in der Form f(x) = vor. Bei der Funktion f(x) stört im Nenner die Zahl 6 vor dem x;bei der Funktion h(x) stört im Nenner die Zahl 3 vor dem x. Das macht die Sache tatsächlich deutlich schwieriger. Bisher hatten wir immer nur Beispiele, bei denen das nicht der Fall war. Das ist führt nun zu dem Problem, dass man die Asymptoten nicht mehr sofort ablesen kann. Man erkennt hier ja bei beiden Funktionen die Definitionslücke nicht direkt, so dass wir auch die senkrechte Asymptote jeweils nicht direkt ablesen können. Daher müssen wir als erstes eine kleine Nebenrechnung für jede der beiden Funktionen machen, um herauszufinden, für welche Werte von x der Nenner Null ergibt.

Nebenrechnung zu f(x) = Nebenrechnung zu h(x) =

| |

| |

Nun kennen wir jeweils die Definitionslücke und somit auch die senkrechte Asymptote.

f(x) hat die senkrechte Asymptote bei x = 1,5 und h(x) bei x = .

Was ist nun aber mit den waagrechten Asymptoten? Die Funktionen liegen ja leider beide nicht in der Form f(x) = vor. Daher ist es für dich vermutlich nicht so einfach die waagrechte Asymptote jeweils zu erkennen. Du kannst hier jedoch die unten folgende Merkregel für Funktionen der Form f(x) = anwenden:

Hinweis:Mit f(x) = sind Funktionen gemeint, deren Funktionsgleichung nur aus einem einzelnen Bruch besteht, also ohne Zahl dahinter oder davor, die subtrahiert oder addiert wird.

Merkregel:

Die x-Achse ist immer genau dann die waagrechte Asymptote einer gebrochenrationalen Funktion, wenn die höchste x-Potenz des Zählers kleiner ist als die höchste x-Potenz des Nenners der Funktionsgleichung. Steht im Zähler der Funktionsgleichung nur eine Zahl ohne x hat die Funktion immer die x-Achse als waagrechte Asymptote. (Vorsicht:Das gilt wirklich nur für Funktionen, deren Funktionsgleichung auf einem kompletten Bruchstrich steht.)

Diese Regel gilt beispielsweise für die Funktionen k(x) = oder l(x) = , aber eben nicht für die Funktionen s(x) = oder t(x) = ! Die Funktionsgleichungen von s(x) und t(x) haben hinter dem Bruch noch eine Zahl, die addiert bzw. subtrahiert wird. Sie stehen also nicht auf einem kompletten Bruchstrich. Nicht die x-Achse, sondern die Geraden y = 7 bzw. y = -2,5 sind die waagrechten Asymptoten von s(x) bzw. t(x).

Die Funktionen k(x) und l(x) erfüllen dagegen die Bedingung:Die Funktionsgleichungen stehen auf einem kompletten Bruchstrich und die höchste x-Potenz des Zählers ist kleiner als die höchste x-Potenz des Nenners. Bei k(x) steht im Zähler als höchste x-Potenz einfach x, also und im Nenner als höchste x-Potenz . Da eine höhere Potenz hat als , ist die Bedingung, dass der Nenner die höhere x-Potenz haben soll, auch erfüllt. Daher ist die x-Achse die waagrechte Asymptote von k(x). Für l(x) gilt entsprechend das Selbe. Bei l(x) steht im Zähler nur die Zahl 3, was man auch als ansehen kann. Im Zähler ist also die einzige und somit gleichzeitig höchste x-Potenz 0. Im Nenner ist bei l(x) die höchste x-Potenz wegen x = einfach 1. Also ist die höchste x-Potenz des Zählers kleiner als die höchste x-Potenz des Nenners. Daher hat auch l(x) die x-Achse als waagrechte Asymptote.

Erläuterung der Merkregel:

Ist bei einem Bruch die höchste x-Potenz des Zählers kleiner als die höchste x-Potenz des Nenners, so nähert sich der Bruch für (vom Betrag her) große x, z.B. x = 1000 oder x = 10000, an den Wert 0 an. Das kannst du ganz leicht selbst überprüfen, indem du sehr große Zahlen, z.B. 1000 oder 10000, für x in die Funktionsgleichung einsetzt und das mit dem Taschenrechner ausrechnest. Je größer x wird, desto näher wird sich das Ergebnis des Bruchs an Null annähern. Man sagt:Der Bruch „geht gegen“ Null. Wird x immer größer, nähert sich das Ergebnis des Bruchs also immer mehr an die Null an, erreicht sie aber nicht.

Was bedeutet dies nun für eine gebrochenrationale Funktion? Steht im Zähler des Bruchs ein Term, dessen höchste x-Potenz kleiner ist als die höchste x-Potenz des Nenners, beispielweise , so wird mit wachsendem x der y-Wert immer kleiner und für sehr, sehr große x wird er fast Null. Der y-Wert nähert sich, wie gesagt, an die Zahl Null an, erreicht sie aber nicht. Für den Graph so einer Funktion bedeutet dies, dass die x-Achse, die ja bekanntlich die Gleichung y = 0 hat, die waagrechte Asymptote ist. Noch ausführlicher wird dies im Kapitel Gebrochenrationale Funktionen (Hyperbeln) erläutert.

Die oben beschriebene Merkregel hilft indirekt sogar bei Funktionen wie z.B. s(x) = oder t(x) = , also bei Funktionen, in deren Gleichung hinter dem Bruch noch eine Zahl steht, die addiert oder subtrahiert wird. Wenn zumindest für den Bruch gilt, dass die höchste x-Potenz des Zählers kleiner ist als die höchste x-Potenz des Nenners, geht der Bruch alleine für große x gegen Null und die ganze Funktion nähert sich damit an die Zahl an, die hinter dem Bruch steht. Die Zahl hinter dem Bruch ergibt dann die waagrechte Asymptote. Deshalb hat s(x) = die Gerade y = 7 als waagrechte Asymptote und entsprechend hat die Funktion t(x) = die Gerade mit der Gleichung y = – 2,5 als waagrechte Asymptote.

Nun aber wieder zurück zu unserer Aufgabe! Wir wollten die waagrechten Asymptoten der beiden Funktionen f(x) = und h(x) = ermitteln, damit wir die Graphen dieser Funktionen nachher leichter zeichnen können. (Die senkrechten Asymptoten, also im Prinzip die Definitionslücken, hatten wir schon berechnet.) Die waagrechte Asymptote von f(x) kannst du nun mit Hilfe der oben beschriebenen Merkregel sicher leicht erkennen. Überlege nun erst ´mal selbst, bevor du weiterliest.

Du hast sicher festgestellt, dass f(x) die x-Achse als waagrechte Asymptote hat, denn die Funktionsgleichung steht auf einem kompletten Bruchstrich und im Zähler steht bloßeine Zahl, aber kein x. Die Zahl 2, die hier im Zähler steht, kann man sich schließlich auch als 2 denken, denn . Daher ist die höchste x-Potenz des Zählers 0. Wegen ist die höchste x-Potenz des Nenners 1. Somit ist die höchste x-Potenz des Zählers kleiner als die des Nenners und die x-Achse ist waagrechte Asymptote von f(x).

Jetzt versuchst du die waagrechte Asymptote der zweiten Funktion h(x) = zu finden.

Hier kannst du die Regel nur indirekt anwenden, da die Funktionsgleichung nicht auf einem gemeinsamen Bruchstrich steht. Aber der Bruch ohne der Zahl dahinter erfüllt die Bedingung, dass die höchste x-Potenz des Zählers kleiner ist als die höchste x-Potenz des Nenners. (Das ist ja immer erfüllt, wenn im Zähler nur eine Zahl steht. Weil bei einer gebrochenrationalen Funktion im Nenner immer x oder eine Potenz von x vorkommt, ist die höchste x-Potenz des Nenners mindestens 1. Steht im Zähler nur eine Zahl, ist die einzige und somit auch höchste x-Potenz des Zählers 0. Dass 0 kleiner ist als 1, braucht eigentlich nicht extra gesagt werden.) Daher geht der Bruch alleine gegen Null und die gesamte Funktionsgleichung in diesem Fall gegen 1, weil zu dem Bruch noch 1 addiert wird. Die waagrechte Asymptote hat also die Gleichung y = 1.Wir haben ja auch oben schon gesagt, dass man einfach die Zahl hinter dem Bruch als waagrechte Asymptote nehmen kann, wenn der Bruch die Bedingung erfüllt, dass die höchste x-Potenz des Zählers kleiner ist als die des Nenners.

Jetzt fassen wir noch einmal alle unsere Ergebnisse zusammen.

f(x) = h(x) =

Senkrechte Asymptote: x = 1,5 Senkrechte Asymptote: x =

Waagrechte Asymptote:y = 0 (x-Achse) Waagrechte Asymptote:y = 1

Die beiden Funktionen liegen zwar nicht ganz in der Form f(x) = vor, weil vor dem x im Nenner noch eine Zahl steht. (Bei f(x) steht vor dem x noch die Zahl 6 und bei h(x) steht vor dem x noch die Zahl 3.) Den prinzipiellen Verlauf des Graphen beeinflussen diese Zahlen jedoch nicht. Daher müssen beide Funktionsgraphen vom Prinzip her dennoch so ähnlich aussehen wie der im Bild 1 (aus Bsp. 1) dargestellte Graph einer Funktion f(x) = mit ungerader Potenz n und positivem a, da bei beiden Funktionen im Nenner keine Klammer mit Quadrat vorkommt (d.h. Potenz n des Nenners ist ungerade) und das Vorzeichen des Zählers bzw. des ganzen Bruchs positiv ist (d.h. ). Unsere Funktionen haben natürlich andere Asymptoten.

(aus Bsp. 1)

Damit kannst du die beiden Funktionsgraphen nun grob skizzieren. Los geht´s! Bitte wirklich selbst probieren!

Wenn dir die oben beschriebenen Überlegungen zum prinzipiellen Verlauf der Graphen zu kompliziert sind, machst du einfach jeweils eine Wertetabelle und zeichnest die Graphen damit. Das geht natürlich genauso, aber es dauert viel länger. Es wäre also schon wichtig, dass du langfristig lernst, nur an Hand der Funktionsgleichung den groben Verlauf des Graphen vorhersagen zu können. Deshalb wurde auch in allen Beispielen immer ausführlich erklärt, auf was man dabei besonders zu achten hat, nämlich das Vorzeichen von a und die Potenz n der Klammer im Nenner.

Entweder hast du nun eine grobe Skizze oder eine genaue Zeichnung der beiden Graphen von f(x) = und h(x) = vor dir. Sie müsste aussehen wie die folgende Abbildung:

Alex:Hier fehlt eine Abbildung! Siehe Blatt!

Abb.:Die Graphen der Funktionen f(x) = und h(x) = mit ihren Asymptoten

Schon an einer groben Skizze lässt sich ablesen, wie oft sich die Graphen schneiden:Offensichtlich existieren zwei Schnittpunkte. Der eine muss eine x-Koordinate haben, die kleiner ist als , weil er links von der senkrechten Asymptote x = liegt. Der andere Schnittpunkt muss eine x-Koordinate haben, die auf jeden Fall größer ist als 1,5 , weil er rechts von der senkrechten Asymptote x = 1,5 liegt. Genau ablesen lassen sich die Koordinaten der Schnittpunkte hier nicht, aber das ist ja in dieser Aufgabe auch gar nicht verlangt. Es ist schließlich nur nach der Anzahl der Lösungen der Bruchgleichung und somit nach der Anzahl der Schnittpunkte von f(x) und h(x) gefragt. Du weißt nun:Die Bruchgleichung hat zwei verschiedene Lösungen. Fertig!

Anmerkung:Zur genauen Ermittlung der Lösungen müsste ein rechnerisches Verfahren verwendet werde. Das graphische Verfahren wäre hier zu ungenau. Das graphische Verfahren verrät dir aber schon einmal, dass sich die Mühe lohnt, eine Rechnung zu machen, da du aus der Zeichnung entnehmen kannst, dass es überhaupt Lösungen der Gleichung gibt, und dass nicht etwa einfach die leere Menge Lösungsmenge der Gleichung ist.

In der Teilaufgabe 4a.) lag dagegen eine Bruchgleichung vor, die gar keine Lösungen hatte, deren Lösungsmenge also einfach die leere Menge ist. Aus der Zeichnung war sofort zu erkennen, dass sich die beiden Graphen nicht schneiden, und dass somit gar keine Lösungen der Bruchgleichung existieren können. Dann brauchst du natürlich gar nicht anfangen zu rechnen, da du ja schon weißt, dass es keine Lösung gibt. Das graphische Verfahren dient daher oft dazu, sich einen Überblick über die Anzahl der möglichen Lösungen zu verschaffen. Wenn du aus der Skizze eindeutig erkennen kannst, dass keine Schnittpunkte und daher auch keine Lösungen der Bruchgleichungen vorhanden sind, kannst du dir jede weitere Rechnung sparen. Die Lösungsmenge ist dann sowieso leer.

Einen ganz besonderen Fall einer Bruchgleichung stellt die nächste Teilaufgabe dar. Einerseits ist sie richtig gemein, aber andererseits auch total leicht. Mal sehen, was du von der Aufgabe hältst! Hier verbirgt sich nämlich noch ein Problem, das wir bisher noch gar nicht besprochen haben.

zu 4c.)

Hier noch einmal die Angabe:

Lösung:

Bevor du hier versuchst, die Gleichung sofort graphisch nach unserem Standartverfahren zu lösen, solltest du die beiden Brüche erst einmal genauer betrachten. Lassen sie sich vielleicht irgendwie vereinfachen? Kann man etwas ausklammern, so dass sich danach vielleicht kürzen lässt?

Es ist dir nun bestimmt aufgefallen, dass man im Zähler des linken Bruchs die Zahl 2 ausklammern kann. Bei dem Bruch auf der rechten Seite der Gleichung kann im Zähler die Zahl 4 und im Nenner die Zahl 2 ausgeklammert werden. Wenn man das macht, erhält man:

Nun fällt dir sicher wieder etwas auf! Nämlich, dass im Zähler und im Nenner beider Brüche jeweils zwei ganz ähnliche Faktoren auftreten. So steht beim linken Bruch im Zähler x – 3 und im Nenner 3 – x und beim rechten Bruch im Zähler 1 – 4x und im Nenner 4x – 1. Es ist also jeweils nur die Reihenfolge genau umgekehrt. Wenn du das Kapitel Definitionsmenge einer Bruchgleichung bereits gelesen hast, dürfte dir das aus der Teilaufgabe 1c) dieses Kapitels bekannt vorkommen. Dort ist auch ausführlich erklärt, warum sich durch das Ausklammern der Zahl -1 bzw. eines Minuszeichens die Reihenfolge einer Differenz umdreht.

Mit diesem kleinen Trick können wir unsere Bruchgleichung so umformen, dass sich nachher kürzen lässt. (Vorsicht:Du darfst dabei die Definitionsmenge nicht vergessen! Sie muss nämlich noch an der ungekürzten Form der Bruchgleichung berechnet werden! Sonst verliert man eventuell eine oder mehrere Definitionslücken.)

Wir klammern jetzt jeweils im Zähler des linken Bruchs als auch im Zähler des rechten Bruchs -1, d.h. ein Minuszeichen, aus. (Wir hätten genauso gut im Nenner das Minuszeichen ausklammern können. Das hätte auch funktioniert. Hauptsache einer der beiden Faktoren dreht sich von der Reihenfolge um. Ob das nur der Zähler oder nur der Nenner ist, ist völlig egal.)

Nun kann man auf beiden Seiten der Gleichung schön kürzen. Bevor wir das machen, ermitteln wir aber noch schnell die Definitionsmenge:

Der Nenner des linken Bruchs ergibt Null, wenn man x = 3 setzt. Bei x = 3 liegt also die erste Definitionslücke. Für welche x der Nenner des rechten Bruchs gleich Null wird erkennt man nicht ganz leicht. Es liegt hier ein Produkt mit den Faktoren 2 und 4x – 1 vor. Du weißt, dass ein Produkt gleich Null ist, wenn einer der Faktoren Null ist. Da der Faktor 2 niemals Null ergibt, muss also der Faktor 4x – 1 gleich Null sein, damit das gesamte Produkt gleich Null wird. Die Zahl 2 darfst du einfach weglassen. Wir müssen also die folgende kleine Nebenrechnung machen:

|

|

Für x = 0,25 wird der Nenner des rechten Bruchs gleich Null;bei x = 0,25 liegt eine Definitionslücke. Der Nenner des anderen Bruchs wird Null für x = 3. Insgesamt hat die ganze Bruchgleichung daher die beiden Definitionslücken x = 0,25 und x = 3. Die Definitionsmenge ist daher: D = ℚ bzw. ab der 9. Klasse: D = ℝ

Nun können wir endlich kürzen:

Upps, wo ist denn hier das x geblieben? Tja, x hat sich hier vollständig herausgekürzt. Es hat sich eine Aussage ergeben, die immer wahr ist, egal was man für x einsetzt, solange x innerhalb der Definitionsmenge liegt. Die Gleichung hat daher unendlich viele Lösungen. die Lösungsmenge ist hier gleich der Definitionsmenge.

L = D = ℚ bzw. ab der 9. Klasse: L = D = ℝ

Graphisch anschaulich bedeutet dies folgendes:

Die linke Seite der Gleichung sehen wir als Funktion f(x) = und die rechte Seite der Gleichung als Funktion h(x) = an. Beide Funktionen sind gebrochenrational, weil sie beide x im Nenner enthalten. Die Graphen von f(x) und h(x) sind allerdings keine Hyperbeln, obwohl es sich um gebrochenrationale Funktionen handelt. Die jeweilige Definitionslücke lässt sich hier nämlich vollständig aus dem Nenner wegkürzen. Solche Definitionslücken sind keine senkrechten Asymptoten, sondern sehen aus wie Löcher im Graph!

Wie sehen nun aber die Graphen der beiden Funktionen aus? Dazu geben wir bei jeder der beiden Funktionen die Definitionsmenge einzeln an und kürzen dann die Funktionsgleichungen.

f(x) = bzw. ab der 9. Klasse:

f(x) =

h(x) = bzw. ab der 9. Klasse:

h(x) =

Der Graph der Funktion f(x) stellt eine waagrechte Gerade mit Loch bei x = 3 dar. Sie verläuft im Abstand 2 unterhalb der x-Achse. Das erkennt man daran, dass sich f(x) = – 2 auch schreiben lässt als f(x) = 0x – 2 und dies stellt schließlich eine Gerade, d.h. eine Funktion in der Form f(x) = mx + t dar. Die Steigung m = 0, daher ist die Gerade waagrecht. Der y-Achsenabschnitt t = – 2, deshalb schneidet die Gerade die y-Achse bei – 2. Da die Funktion f(x) aber nicht in ganz ℚ bzw. ganz ℝ definiert ist, sondern nur für bzw. muss an der Stelle x = 3 eine Definitionslücke sein. Diese Lücke sieht aus wie eine Loch in der Gerade. Es handelt sich dabei um einen einzelnen Punkt, der fehlt. Die Definitionslücke wird daher als „offener Kringel“ in der Zeichnung markiert.

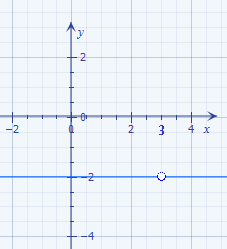
Abb.:Graph der Funktion f(x) = für

Entsprechend stellt auch der Graph der Funktion h(x) = eine waagrechte Gerade mit Loch dar, die ebenfalls im Abstand 2 unterhalb der x-Achse verläuft. Allerdings ist hier die Definitionslücke bei x = 0,25. Daher liegt auch das Loch hier bei x = 0,25.

Abb.:Graph der Funktion h(x) = für

Schneidet man nun die Graphen von f(x) und h(x) miteinander, so gibt es unendlich viele gemeinsame Punkte, die alles die y-Koordinate y = – 2 haben. Die beiden Löcher (0,25|- 2) und (3|- 2) sind natürlich ausgeschlossen und gehören daher nicht zur Lösung der Bruchgleichung. Die x-Koordinate der gemeinsamen Punkte kann somit alle beliebigen Werte annehmen außer die Werte 0,25 und 3, weil hier die Definitionslücken sind. Auf jeden Fall gibt es hier unendlich viele gemeinsame Punkte der Graphen von f(x) und h(x);daher hat die Bruchgleichung unendlich viele Lösungen.

Ich muss zugeben, dass diese Aufgabe echt schwierig war. Sie stellt einen absoluten Extremfall dar. Oft wird so etwas bestimmt nicht gefragt, doch wer weißauf welche Ideen Lehrer in Schulaufgaben kommen. Daher wurde auf dieser website auch einmal so eine Bruchgleichung vorgestellt.

Was du dir auf jeden Fall merken solltest:Kannst du eine Definitionslücke bei einer gebrochenrationalen Funktion vollständig aus dem Nenner kürzen, dann handelt es sich bei dieser Lücke um ein „Loch“ und nicht um eine senkrechte Asymptote! Ausführlicher wird das bei den Definitionslücken besprochen.

Nun zu einem weiteren, ebenfalls nicht so leichten Beispiel.

5. Bsp.:

Ermittle mit Hilfe einer Zeichnung für welche Werte von t die folgende Bruchgleichung genau eine, keine bzw. zwei verschiedene Lösungen besitzt! Ohne Rechnung, nur mit Überlegung!

Lösung:

Jetzt wird es schon etwas schwieriger. Das Problem ist dabei natürlich das Auftreten des Buchstabens t zusätzlich zur Variablen x.

Vorsicht:t ist ein sogenannter Scharparameter, kurz Parameter genannt, und keine Variable wie x! Zwischen den Begriffen „Parameter“ und „Variable/Lösungsvariable“ ist ein riesiger Unterschied! x ist die Lösungsvariable, d.h. man soll die Gleichung nach x auflösen und nicht etwa nach t. Die Lösungsvariable x kann dabei allerdings nur in Abhängigkeit vom Parameter t berechnet werden. (Würde man die Gleichung rechnerisch nach x auflösen, käme als Lösung für x ein Ausdruck heraus, der den Parameter t enthält. Das brauchen wir hier aber nicht machen, weil es in der Aufgabenstellung nicht verlangt ist.)

Der Parameter t ist zwar eine momentan unbekannte Zahl, aber eine feste Zahl. Man könnte auch sagen:t ist eine Konstante, also irgendeine bestimmte (konstante) Zahl. Wir werden uns das Problem mit dem t gleich noch genauer ansehen. Stelle dir vorerst für t einfach irgendeine konkrete Zahl vor und frage dich, wie dann vorgehen würdest, um die Gleichung graphisch zu lösen. (Wirklich einsetzen darfst für t jetzt natürlich nichts, denn wir suchen ja diejenigen Werte von t, für die sich eine, keine oder zwei Lösungen ergeben.) Naja, was machen wir denn immer, wenn wir eine Bruchgleichung graphisch lösen sollen? Hier sollen wir die Gleichung zwar nicht lösen, sondern herausfinden, für welche t eine, keine oder zwei Lösungen existieren. Trotzdem nehmen wir wieder unser Standartverfahren zur graphischen Lösung von Bruchgleichungen:

Wir betrachten also die linke Seite und die rechte Seite der Gleichung jeweils als Funktionen, die wir dann versuchen zu schneiden:

Hier noch einmal die Gleichung:

Dann sind die beiden Funktionen logischerweise:

f(x) =

Die Gleichung würde bei der Schnittpunktberechnung entstehen, nämlich durch das Gleichsetzen der Hyperbel f(x) = mit der Geradenschar . Dass hier eine Schar von Funktionen vorliegt, erkennst du am Auftreten des zusätzlichen Buchstabens t in der Funktionsgleichung. Aber was ist denn eigentlich so eine Geradenschar? Eine Geradenschar besteht aus vielen einzelnen Geraden. Je nach dem, was für den Scharparameter t eingesetzt wird, erhält man eine andere Gerade der Schar. Man legt zuerst t fest und kann dann diese spezielle Schargerade zeichnen. Mehr dazu auch im Kapitel Geradenscharen!

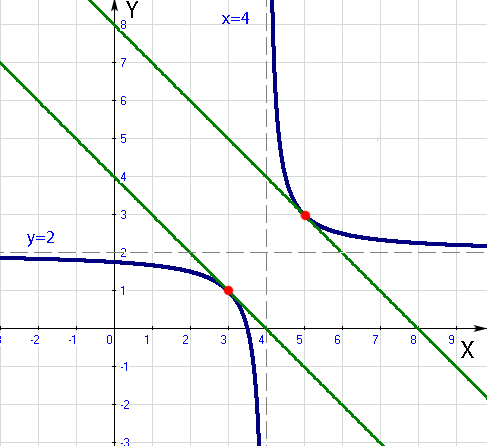
Hier liegt eine besondere Geradenschar vor, eine sogenannte Parallelenschar, da die Steigung m = – 1 nicht vom Scharparameter t abhängt. In anderen Worten:Die Steigung m ist bei jeder Schargerade gleich, weil der Parameter t nur beim y-Achsenabschnitt vorkommt, aber nicht in der Steigung m, und daher sind alle Geraden der Schar parallel. Geraden mit gleicher Steigung sind schließlich immer parallel. Der Scharparameter verändert hier also nur den y-Achsenabschnitt. Je nach dem, was für t eingesetzt wird, schneidet die Schargerade die y-Achse weiter oben oder weiter unten. t schiebt praktisch die Gerade nur nach oben oder unten. Alle Geraden der Schar verlaufen parallel zur Winkelhalbierenden des II. und IV. Quadranten. Das liegt daran, dass sie alle die Steigung m = – 1 besitzen. Will man das Steigungsdreieck einer dieser Geraden zeichnen, muss man ja immer 1 nach rechts und 1 nach unten gehen. Damit du dir das besser vorstellen kannst, sind in der folgenden Abbildung einige ausgewählte Geraden der Schar in einem gemeinsamen Koordinatensystem dargestellt. Für t wurden dabei die Werte -1, 0;1;2 ;3 und 4 gewählt. Natürlich könnte t auch andere Werte annehmen. Es handelt sich hierbei um eine absolut beliebige Auswahl. Man hätte genauso gut irgendwelche Dezimalzahlen oder Brüche nehmen können, doch dann hätten sich die Geraden nicht so schön zeichnen lassen.

Hinweis zur Schreibweise: Der Index 4, d.h. die tiefergestellte kleine 4 hinter dem g, bedeutet, dass für den Parameter t hier der Wert 4 in die Funktionsgleichung eingesetzt wurde. Der Index gibt also immer an, was für den Parameter eingesetzt wurde.

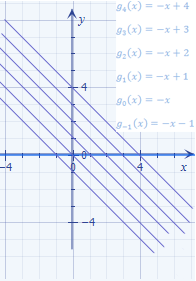
Abb.:Einige Geraden der Schar

Nun kannst du dir die Parallelenschar hoffentlich etwas besser vorstellen. Zur Lösung dieser Aufgabe hättest du diese Schargeraden übrigens nicht unbedingt zeichnen müssen. Die soeben gezeigte Abbildung soll dir nur dabei helfen, dass du dir etwas Konkretes unter der Schar vorstellen kannst.

Nun zurück zu unserer Fragestellung:Für welche Werte von t hat die angegebene Gleichung eine, zwei oder keine Lösung? Dies entspricht eigentlich der Frage, für welche Werte von t die Hyperbel f(x) = mit der Geradenschar einen, zwei oder keinen gemeinsamen Punkt besitzt. Daher zeichnen wir erst einmal die Hyperbel in ein Koordinatensystem. Das kannst du bestimmt auch alleine. Also, Papier und Bleistift zur Hand nehmen und selbst versuchen! Bevor du mit der Zeichnung beginnst, überlegst du dir natürlich die Asymptoten.

Platzbedarf für die Zeichnung:

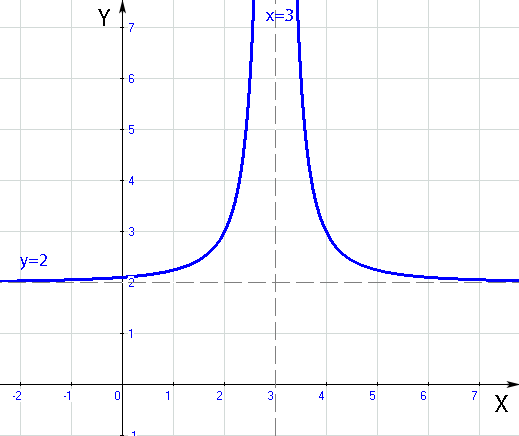
Wenn du es richtig gemacht hast, hast du für die Asymptotengleichungen von f(x) = Folgendes erhalten:

Senkrechte Asymptote: x = 4

Waagrechte Asymptote: y = 2

Der von dir gezeichnete Graph sollte so ähnlich aussehen wie der in der folgenden Abbildung.

Abb.:Graph der Hyperbel f(x) =

Jetzt musst du dir überlegen, für welche Werte von t sich genau ein gemeinsamer Punkt, zwei gemeinsame Punkte oder gar kein gemeinsamer Punkt der Hyperbel und einer der Schargeraden ergibt. Wir wissen wegen m = -1, dass alle Schargeraden parallel zur fallenden Winkelhalbierenden y = – x sind. Nun nimmst du dein Geodreieck zur Hand und legst es so auf deine Zeichnung, als wolltest du diese Winkelhalbierende zeichnen. Die Kante des Geodreiecks stellt praktisch eine der Schargeraden dar – genau genommen die Schargerade mit t = 0. Durch Verschiebung senkrecht nach oben oder unten erhältst du andere Geraden der Schar. (Alle Schargeraden von verlaufen ja parallel zu y = – x.) Als nächstes wollen wir uns überlegen, für welche Werte von t genau ein gemeinsamer Punkt existiert. Dazu verschiebst du das Geodreieck so lange entlang der y-Achse senkrecht nach oben bzw. unten, bis es die Hyperbel in genau einem Punkt berührt. Diese Schargerade zeichnest du ein und liest den y-Achsenabschnitt t aus deiner Zeichnung ab. Du wirst feststellen, dass es dafür zwei Möglichkeiten gibt. Einmal berührt die Gerade den linken Hyperbelast und einmal den rechten Ast. So erhalten wir nun zwei Werte von t:Für t = 4 und für t = 8 berührt die Gerade die Hyperbel. Du zeichnest nun auch noch die zweite Schargerade ein, welche die Hyperbel berührt. Zu deiner Kontrolle:Die Koordinaten des Berührpunkts lauten für t = 4 B(3|1) bzw. für t = 8 B*(5|3).

Abb.:Der Graph der Hyperbel f(x) = hat mit den Geraden und jeweils genau einen Punkt gemeinsam.

Jetzt wissen wir:Für t = 4 und für t = 8 gibt es genau einen gemeinsamen Punkt von Hyperbel und Schargerade. Somit hat die Gleichung für t = 4 und für t = 8 genau eine Lösung.

Nun überlegst du dir als nächstes, wo die Gerade liegen muss, damit sie mit der Hyperbel zwei gemeinsame Punkte hat. Alle Schargeraden, die unterhalb der Gerade liegen, schneiden den linken Hyperbelast in zwei Punkten. Außerdem schneiden auch alle Schargeraden, die oberhalb der Gerade liegen, den rechten Hyperbelast in zwei verschiedenen Punkten. Die Schnittpunkte können zwar außerhalb des von dir gezeichneten Koordinatensystems liegen, doch das macht nichts. Es geht ja nur darum, dass es überhaupt zwei Schnittpunkte gibt. Wo diese Punkte liegen, ist egal. Das bedeutet, dass für oder zwei Schnittpunkte existieren. Somit muss die Gleichung für oder zwei Lösungen besitzen.

Als letztes müssen wir untersuchen, für welche Werte von t die Gleichung gar keine Lösung hat. Es bleibt nur noch die Möglichkeit übrig, d.h. dass t zwischen 4 und 8 liegt. Anschaulich erkennst du das in deiner Zeichnung daran:Liegt eine Schargerade oberhalb von und gleichzeitig unterhalb von , also zwischen den beiden eingezeichneten Schargeraden, hat sie mit der Hyperbel keinen Punkt gemeinsamen. Anders ausgedrückt:t muss zwischen 4 und 8 liegen, damit die Gerade die Hyperbel überhaupt nicht schneidet. Daher hat die Gleichung für keine Lösung.

Zusammenfassung:

Anzahl der Lösungen der Gleichung :

1 Lösung für t = 4 und für t = 8

2 Lösungen für oder oder in Intervallschreibweise:t

0 Lösungen für oder in Intervallschreibweise:t

Der folgende Teil dieses Kapitels eignet sich nur für Schüler, die im Unterricht bereits Parabeln gelernt haben. (Nur für Schüler ab der 9. Klasse G8 oder R6 mathematischer Zweig bzw. ab der 10. Klasse R6 nicht-mathematische Zweige)

6. Bsp.:

Ermittle graphisch die gemeinsamen Punkte der folgenden beiden Funktionen!

f(x) = p(x) =

Lösung:

Der Graph der Funktion f(x) ist eine Hyperbel, da die Funktionsgleichung von f die Variable x im Nenner enthält, d.h. f(x) ist eine gebrochenrationale Funktion. Der Graph der Funktion p(x) ist dagegen eine Parabel, da es sich bei p(x) um eine quadratische Funktion handelt, also um eine Funktion der Form p(x) = mit . In dieser Aufgabe ist nach den gemeinsamen Punkten der Hyperbel f(x) und der Parabel p(x) gefragt. Im Prinzip ist dies fast das Gleiche, als wäre nach der Lösung der Bruchgleichung gefragt gewesen. Es müssen nur zusätzlich zu den x- Koordinaten auch jeweils die y-Koordinaten der gemeinsamen Punkte angegeben werden. Da hier eine graphische Lösung verlangt ist, werden einfach jeweils die x- und y- Koordinate der gemeinsamen Punkte aus der Zeichnung abgelesen. Dazu musst du bloßdie Graphen der Funktionen f(x) und p(x) in ein gemeinsames Koordinatensystem zeichnen. Dann kannst du sehen, welche Punkte auf beiden Funktionen liegen.

Um die Hyperbel f(x) = zeichnen zu können, überlegst du dir vorab die Gleichungen der Asymptoten. Das ist ja nicht schwer, da die Funktion bereits in der Form f(x) = vorliegt.

Die Gleichungen der Asymptoten von f(x) = lauten:

Senkrechte Asymptote: x = – 3

Waagrechte Asymptote: y = 1

Das Vorzeichen des Zählers a bzw. des Bruchs ist positiv und die Potenz n = 2 ist gerade. Daher verläuft der Graph von f(x) prinzipiell ähnlich wie der im Bild 3 (aus Bsp. 1) gezeigte Graph, natürlich mit einer ganz anderen senkrechten Asymptote, vergleiche dazu die oben aufgeführten Asymptoten.

Bild 3 (aus Bps. 1)

Jetzt müsstest du den Graph von f(x) eigentlich schon grob skizzieren können. Wenn du noch ein paar Funktionswerte berechnest, kannst du die Hyperbel auch gleich genau zeichnen. Berechne beispielsweise f(-5), f(-4), f(-3,5), f(-2,5), f(-2), f(-1) und eventuell noch f(0)! Also los geht’s!

Danach musst du in das selbe Koordinatensystem die Parabel p(x) einzeichnen. Es handelt sich hier wegen a = -1 um eine nach unten geöffnete Normalparabel. Wenn wir ihren Scheitel wüssten, könnten wir sie mit einer Schablone schnell zeichnen. Daher berechnen wir vorweg den Scheitel von p(x). Wir verwenden die Quadratische Ergänzung (zur Scheitelberechnung).

p(x)

p(x)

p(x)

p(x) =

p(x) =

p(x) =

Nun liegt die Parabel in ihrer Scheitelform vor. Wir können ihren Scheitel also bequem ablesen:Scheitel S(- 3|3)

Jetzt zeichnest du die Parabel mit Hilfe einer Schablone für Normalparabeln in deine Skizze, die schon die Hyperbel enthält. Achte dabei darauf, dass du die Schablone wirklich exakt anlegst! Ansonsten bekommst du sehr große Ungenauigkeiten bei den Schnittpunkten. Also unbedingt sehr sauber zeichnen!

So sollte deine Zeichnung aussehen:

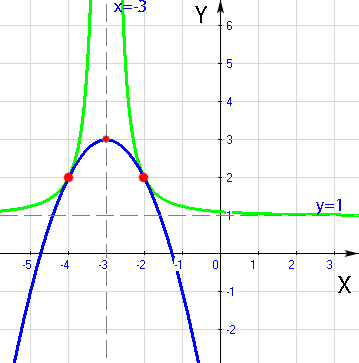
Abb.:Die Graphen der Funktionen f(x) = und p(x) = mit ihren gemeinsamen Punkten und

Aus der Zeichnung lassen sich gut die gemeinsamen Punkte beider Graphen ablesen. Sie haben die Koordinaten und . Damit ist die Aufgabe gelöst!

Das soll nun reichen an Beispielen für das graphische Lösungsverfahren von Bruchgleichungen. Wichtiger als das graphische Lösungsverfahren sind langfristig sicher die Rechnerischen Lösungsverfahren von Bruchgleichungen. Du brauchst sie nicht nur in der Mathematik, sondern manchmal auch in der Physik. Das graphische Verfahren wäre da einfach zu ungenau, da die Lösungen hier oft nicht aufgehen.

• Page 2 of 2
• « Previous
• 1
• 2
• Next »