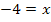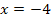Rechnerische Lösungsverfahren von Bruchgleichungen
Die Probe stimmt, damit ist unsere Gleichung wirklich für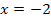 
erfüllt und die Lösungsmenge ist tatsächlich L = 
.
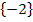Wir fassen unsere Vorgehensweise noch einmal stichpunktartig zusammen:
Allgemeine Anleitung zur rechnerischen Lösung von Bruchgleichungen:
|
zu 1b.)
Hier noch einmal die Angabe:
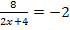
Lösung:
Wir verfahren, wie in der Anleitung beschrieben.
1. Definitionsmenge ermitteln:
Entweder man setzt den Nenner sofort gleich Null und berechnet die Definitionslücke, indem man das einfach nach x auflöst. Oder man klammert erst einmal im Nenner die Zahl 2 aus und kürzt sie dann. Wir entscheiden uns hier für die Variante „Ausklammern und Kürzen“, weil sich die Bruchgleichung dadurch nachher etwas leichter lösen lässt.
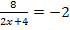
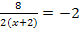
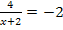
Nun erkennt man, dass die Definitionslücke bei x = – 2 liegt, da der Nenner für x = – 2 Null ergibt. Die Definitionsmenge lautet daher:D = ℚ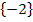
Ausnahmsweise haben wir hier die Definitionsmenge an der gekürzten Bruchgleichung ermittelt. Das Kürzen der Zahl 2 führt ja zu keiner Veränderung der Definitionsmenge. Eine Zahl darfst du grundsätzlich kürzen, bevor du die Definitionsmenge ermittelst, aber besser keine Faktoren, die x enthalten.
2. Hauptnenner aller Brüche bilden, die in der Gleichung vorkommen:
Weil in dieser Gleichung nur ein Bruch vorkommt, ist der Hauptnenner natürlich der Nenner dieses Bruchs, also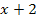 
. (Wir gehen nun von der gekürzten Gleichung aus.)
3. Mit dem Hauptnenner auf beiden Seiten der Gleichung multiplizieren, d.h. bei allen vorkommenden Brüchen jeweils den Zähler mit dem Hauptnenner multiplizieren
| 
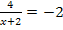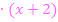
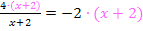
4. Soweit möglich kürzen 
Gleichung, die kein x mehr im Nenner hat
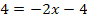
5. Diese Gleichung nach x auflösen
| 
| 
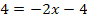
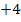
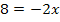
