Lagebeziehungen zwischen zwei Parabeln
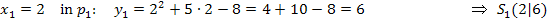
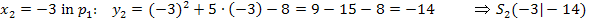
Wir haben die Schnittpunkte berechnet, damit ist die Aufgabe gelöst.
2. Bsp.:
Zeige, dass sich die Parabeln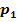 
und 
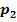berühren! Berechne auch die Koordinaten des Berührpunktes B!
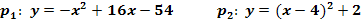
Lösung:
Zuerst setzen wir die Parabeln wieder gleich. Dann vereinfachen wir so weit möglich. Vorsicht:Denke an die zweite binomische Formel beim Auflösen der Klammer! Wir stellen die Gleichung nach Null um, da es sich um eine gemischtquadratische Gleichung (Gleichung mit 
und x) handelt. Nun liegt die Gleichung in der Form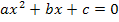 
vor und wir können die Diskriminante 
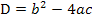ermitteln. Um zu zeigen, dass sich die Parabeln berühren, genügt es zu zeigen, dass sich für die Diskriminante D = 0 ergibt. Aus dem Wort „berühren“ geht schließlich eindeutig hervor, dass es nur einen gemeinsamen Punkt der Parabeln, also genau eine Lösung unserer Gleichung geben darf. Wie du weißt, hat eine gemischtquadratische Gleichung immer dann genau eine Lösung, wenn D = 0 ist. Dann fangen wir ´mal an!
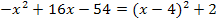
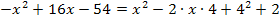
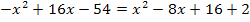
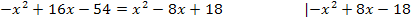
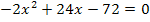
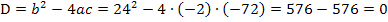
D = 0 
Parabeln berühren sich
Somit haben wir den ersten Teil der Aufgabe gelöst:Wir haben gezeigt, dass sich die beiden Parabeln berühren. Jetzt müssen wir allerdings noch die Koordinaten des Berührpunktes B ermitteln. Um die x-Koordinate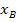 
des Berührpunktes zu berechnen, setzen wir nun in die Mitternachtsformel ein. Die Diskriminante haben wir ja mit D = 0 schon berechnet;wir setzen daher in die folgende Form der Mitternachtsformel ein:
Mitternachtsformel: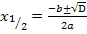 
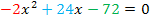
a b c
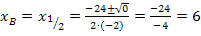
Jetzt fehlt nur noch die y-Koordinate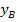 
des Berührpunktes B. Wir setzen 
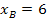in eine der beiden Parabelgleichungen 
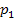oder 
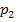ein.
Vorsicht:Nicht in die Gleichung einsetzen, die durch das Gleichsetzen der Parabeln entstanden ist!
Wir entscheiden uns dafür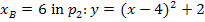 
einzusetzen:
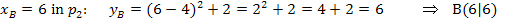
Nun ist der Berührpunkt berechnet und wir sind fertig.
3. Bsp.:
Beweise, dass die Parabeln 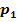und 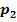keinen Punkt gemeinsamen haben!
Lösung:
Wir setzen die Parabeln wieder gleich. Danach lösen wir die Gleichung nach Null auf. Dann kann die Diskriminante D berechnet werden. Um zu zeigen, dass kein Schnittpunkt der beiden Parabeln existiert, müssen wir nur zeigen, dass die Diskriminante D negativ ist.
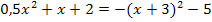
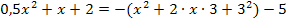
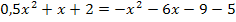
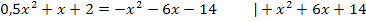
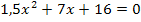
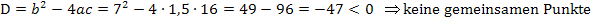
Damit ist die Aufgabe bereits gelöst.
