Lagebeziehungen zwischen zwei Parabeln
Nun wissen wir, dass die beiden Funktionen für k = 9 oder k = 2 genau eine Punkt gemeinsam haben. Die beiden anderen Fälle, also kein oder zwei gemeinsame Punkte, können wir nun in Angriff nehmen. Wir setzen einmal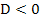 
und einmal 
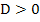. Leider entstehen dadurch in dieser Aufgabe (das muss nicht immer so sein) quadratische Ungleichungen, die nicht so einfach zu lösen sind wie quadratische Gleichungen.
Damit die beiden Funktionen keine Punkte gemeinsam haben, muss gelten:
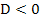
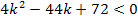
Quadratische Ungleichungen können graphisch oder rechnerisch mit Hilfe einer Fallunterscheidung gelöst werden. Das graphische Verfahren ist eindeutig zu bevorzugen, da es wesentlich schneller und einfacher ist. Daher wählen wir hier diese Methode.
Graphisches Lösungsverfahren für die Quadratische Ungleichung:
Wir stellen uns die linke Seite der Ungleichung als Parabel vor. Vorsicht:Diese Parabel hat nichts mit den ursprünglich gegebenen Parabeln zu tun;das ist eine völlig neue Parabel mit der Variablen k. Dabei ist k nicht mehr Parameter (also nicht mehr eine feste Zahl), sondern Variable! In anderen Worten:k entspricht jetzt quasi x;d.h. nach k soll aufgelöst werden. Wir nennen die neue Parabel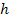 
.
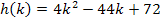
Da der Öffnungsfaktor a = 4 positiv ist, handelt es sich bei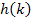 
um eine nach oben geöffnete Parabel. Die Nullstellen von h berechnen sich mit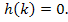 
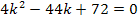
Diese Gleichung haben wir oben bereits gelöst. Wir wissen daher bereits:k = 9 und k = 2 sind die Lösungen dieser Gleichung. Die Parabel 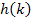besitzt die Nullstellen 
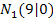und 
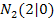. Nun können wir die Parabel h skizzieren. Auf die genaue Form, also die Breite der Parabel oder den Scheitel, kommt es hierbei gar nicht an. Wichtig ist nur, dass wir eine nach oben geöffnete Parabel mit den Nullstellen 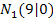und 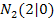zeichnen.
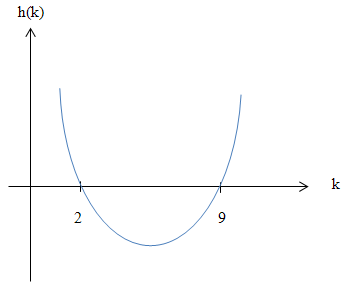
Aus dieser Skizze können wir nun bequem die Lösung der Ungleichung 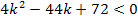ablesen. Die linke Seite der Ungleichung wird ja durch die Parabel 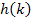dargestellt. Wir müssen uns daher fragen, für welche Werte von k sich 
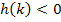ergibt. 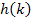ist nichts anderes als der y-Wert der Parabel. Es muss also 
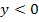sein, d.h. die Parabel unterhalb der k-Achse (sonst x-Achse) liegen. Das ist aber nur für 
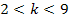der Fall. Statt dessen kann man auch schreiben:k 
]2;9[
Für 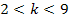bzw. k ]2;9[ gilt also 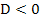und somit haben die ursprünglich gegebene Parabel p und die Schar 
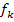nur für diese Werte von k keine gemeinsamen Punkte.
Den letzten zu bearbeitenden Fall, nämlich, dass die ursprünglich gegebene Parabel p und die Schar 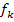zwei verschiedene Punkte gemeinsam haben, bearbeiten wir analog, nur mit .
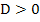