Parabelscharen
Die beiden Nullstellen fallen also zusammen. Es liegt deshalb bei k = 0 ein Sonderfall vor, die Scharparabel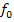 
hat als einzige der gesamten Schar nur eine Nullstelle, nämlich N(0|0). Zusammenfassend kann man schreiben:
für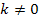 
: Zwei verschiedene Nullstellen 
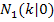und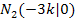 
für k = 0: Eine einzige Nullstelle N(0|0)
So eine gesonderte Untersuchung verschiedener Fälle nennt man Fallunterscheidung. Die Fallunterscheidung wird noch in vielen weiteren Aufgaben mit Funktionenscharen sehr wichtig werden. Da sie häufig zu Problemen führt, weil ihre Notwendigkeit von vielen Schülern gar nicht erkannt wird, wurde sie bereits in diesem ersten, relativ einfachen Beispiel schon einmal erwähnt. (Ob dieses Beispiel wirklich einfach war, das mag manch Schüler sicher etwas anders beurteilen! Aber Scharen sind zu Beginn eben immer schwierig. Da ist es umgekehrt für den Lehrer schwierig, ein lehrreiches, aber einfaches Beispiel zu finden. Sorry, falls es zu schwer war!)
Da bekanntlich (gerade in Mathe) nur Übung den Meister macht, man als Schüler aber nur üben kann, wenn man einmal gezeigt bekam, wie es geht, hier gleich noch ein weiteres Beispiel. Klar wäre es noch besser, wenn du alleine auf die Lösung kommst. Versuche einfach die nächste Aufgabe alleine zu rechnen, ohne vorher die Lösung anzuschauen. Falls es noch nicht klappt oder zumindest zur Kontrolle, folgt gleich danach die Lösung. Nur Mut! Schlimmstenfalls stimmt deine Rechnung nicht, aber es geht ja jetzt nicht um eine Note in einer Prüfung, sondern nur darum, dass du zum Üben kommst. Aus Fehlern lernt man bekanntlich am besten und besser jetzt einen Fehler machen als in einer Schulaufgabe!
2. Bsp.:
Ermittle die Nullstellen der Parabelschar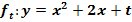 
in Abhängigkeit von t! Gib auch die Anzahl der Nullstellen in Abhängigkeit von t an! (Fallunterscheidung)
Lösung:
Wir setzen wie schon im ersten Beispiel gezeigt, die Funktion gleich Null, um die Nullstellen zu berechnen. Es soll in Abhängigkeit vom Scharparameter t gerechnet werden;wir dürfen also für t keine konkrete Zahl einsetzen. Wir denken uns jedoch t wieder als feste Zahl. Der Scharparameter stellt ja immer eine Konstante dar. t wird vermutlich in der Lösung, d.h. bei den gesuchten Nullstellen, noch auftreten.
y = 0
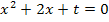
Nun ist wieder eine gemischtquadratische Gleichung entstanden, da die Variable x zum Quadrat und ohne Potenz auftritt. Wie du weißt, lassen sich solche Gleichungen mit der Mitternachtsformel lösen.
Zur Erinnerung:
