Die e-Funktion und ihre Umkehrfunktion die ln-Funktion
Die Funktion 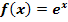 wird als natürliche Exponentialfunktion, kurz e-Funktion, bezeichnet. Sie ist eine der wichtigsten Grundfunktionen der Analysis. Von ihr leiten sich beispielsweise die Funktionen des Typs
wird als natürliche Exponentialfunktion, kurz e-Funktion, bezeichnet. Sie ist eine der wichtigsten Grundfunktionen der Analysis. Von ihr leiten sich beispielsweise die Funktionen des Typs 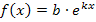 (mit
(mit 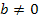 und
und 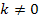 ) ab, welche bei der mathematischen Behandlung von Wachstums- bzw. Zerfallsprozessen eine wichtige Rolle spielen.
) ab, welche bei der mathematischen Behandlung von Wachstums- bzw. Zerfallsprozessen eine wichtige Rolle spielen.
Die Umkehrfunktion von 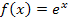 ist die Funktion
ist die Funktion 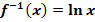 . Sie wird natürliche Logarithmusfunktion, kurz ln-Funktion, genannt. (Die Abkürzung ln kommt vom lateinischen „logarithmus naturalis“, auf Deutsch eben „natürlicher Logarithmus“.) Genauso wichtig wie die e-Funktion ist auch die ln-Funktion.
. Sie wird natürliche Logarithmusfunktion, kurz ln-Funktion, genannt. (Die Abkürzung ln kommt vom lateinischen „logarithmus naturalis“, auf Deutsch eben „natürlicher Logarithmus“.) Genauso wichtig wie die e-Funktion ist auch die ln-Funktion.
Für jeden Schüler ab der 11. Klasse G8 oder 12. Klasse mathematisch-technischer Zweig der FOS/BOS sind diese zwei Funktionen und alles rund herum ein absolutes Muss für das Mathe-Abitur! Eine der beiden Funktionen oder eine Abwandlung davon kommt mit hundertprozentiger Wahrscheinlichkeit auch in deiner Abi- bzw. Fachabiprüfung dran!
In diesem Kapitel werden die e- und ln-Funktion sowie ihre Anwendungen ausführlich an Hand vieler Beispiele besprochen.
Kurzübersicht über den Inhalt dieses Kapitels:
|
Übersicht über den Stoff dieses Kapitels mit Erläuterungen
· Das Wichtigste zur e-Funktion : Die Einführung der Eulerschen Zahl e, Definitions- und Wertemenge der Funktion 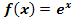 , ihre Grenzwerte im Unendlichen, ihre Ableitungs- und Stammfunktion, sowie der Verlauf des Graphen der e-Funktion werden in diesem Abschnitt behandelt. Außerdem wird hier erklärt, durch welche Abbildungen (Verschiebung, Stauchung, Streckung) sich der Graph der Funktion , ihre Grenzwerte im Unendlichen, ihre Ableitungs- und Stammfunktion, sowie der Verlauf des Graphen der e-Funktion werden in diesem Abschnitt behandelt. Außerdem wird hier erklärt, durch welche Abbildungen (Verschiebung, Stauchung, Streckung) sich der Graph der Funktion 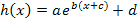 aus dem Graph der Funktion aus dem Graph der Funktion 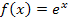 herleiten lässt. herleiten lässt.
· Das Wichtigste zur ln-Funktion: Eine Kurz-Wiederholung des Logarithmus im Allgemeinen und den Logarithmus-Rechengesetzen für alle, die nicht so recht wissen, was ein Logarithmus eigentlich überhaupt ist, und die Einführung des natürlichen Logarithmus · Definitionsmenge ermitteln bei e- und ln- Funktionen: Hier wird an Hand vieler Beispiele erklärt, wie du auch bei schwierigeren Funktionen mit · Grenzwerte von e- und ln-Funktionen: Grenzwerte mit · Nullstellenberechnung von e- und ln-Funktionen: Dass man die Nullstellen einer Funktion durch Gleichnullsetzen des Funktionsterms berechnet, ist dir sicher klar. Doch wie löst man Gleichungen mit · Berechnung der Extrema von e- und ln-Funktionen: Hier wird erklärt, wie man bei einer e-Funktion oder ln-Funktion die erste Ableitung bildet. Außerdem wird die Untersuchung des Monotonieverhaltens und die Berechnung der Extrema solcher Funktionen besprochen. Du erfährst auch, wie man eine Tangentengleichung bei gegebenem Berührpunkt oder von einem Punkt außerhalb des Graphen aufstellt. · Berechnung der Wendepunkte von e- und ln-Funktionen: (Nur für Schüler, die im Unterricht die zweite Ableitung · Komplette Kurvendiskussion bei e- und ln-Funktionen: An Hand einiger ausgewählter Beispiele wird in diesem Abschnitt die ganze Kurvendiskussion von e- und ln-Funktionen gezeigt. Von der Definitionsmenge, über die Untersuchung des Verhaltens von · Funktionenscharen mit e- oder ln:Tritt im Funktionsterm neben der Variablen x noch zumindest ein weiterer Buchstabe auf, z.B. a oder t, liegt eine Funktionenschar vor. Viele Berechnungen müssen dabei in Abhängigkeit vom Scharparameter a bzw. t durchgeführt werden;d.h. man darf für a bzw. t keine konkrete Zahl einsetzen. Man rechnet also einfach so, als wäre a bzw. t eine feste Zahl, auch wenn man sie nicht kennt. Leider müssen dabei oft Fallunterscheidungen durchgeführt werden, was die Sache erheblich schwieriger macht. Wie man solche Aufgaben löst, wird in diesem Teil gezeigt. Oft finden sich auch Fragestellungen folgender Art:„Für welche Werte von a hat die Funktion genau eine Nullstelle?“ Oder: „Für welche Werte von a hat die Funktion mindestens einen Punkt mit waagrechter Tangente?“ Wie du solche Aufgaben lösen kannst, erfährst du auch in diesem Abschnitt. · Anwendungsaufgaben der natürlichen Exponentialfunktion: Zu den häufigsten Anwendungen der e-Funktion zählen Aufgaben mit Wachstums- oder Abklingprozessen. Besonders wichtig für das Matheabi ist das sogenannte „stetige Wachstum“. Funktionen der Form |
Notwendige Vorkenntnisse:
Du solltest wissen, wie man eine Kurvendiskussion zumindest bei einfacheren Funktionen durchführt. Die Begriffe „Grenzwert“, „Ableitung“ und „Extrema/Extrempunkte“ sollten dir geläufig sein. Näheres dazu im Kapitel:Einführung in die Differenzialrechnung

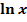 im Speziellen bilden den Anfang dieses Teils. Anschließend wird die ln-Funktion
im Speziellen bilden den Anfang dieses Teils. Anschließend wird die ln-Funktion 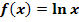 und ihr Graph mit ihrer Definitions- und Wertemenge, ihren Grenzwerten, ihrer Ableitungs- und Stammfunktion besprochen. Im Anschluss beschäftigen wir uns mit Verschiebungen, Stauchungen bzw. Streckungen des Graphen von
und ihr Graph mit ihrer Definitions- und Wertemenge, ihren Grenzwerten, ihrer Ableitungs- und Stammfunktion besprochen. Im Anschluss beschäftigen wir uns mit Verschiebungen, Stauchungen bzw. Streckungen des Graphen von 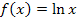 und Spiegelungen an den Achsen.
und Spiegelungen an den Achsen.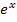 oder
oder 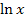 (bzw. Abwandlungen davon) die maximale Definitionsmenge finden kannst. Die korrekte Definitionsmenge ist Grundvoraussetzung für die Berechnung der jeweiligen Grenzwerte. Ohne Kenntnis der Definitionsmenge kannst du das Verhalten einer Funktion an den Rändern ihrer Definitionsmenge nicht untersuchen. Daher ist dieser Teil eine wichtige Grundlage für die nachfolgende Grenzwertberechnung und die gesamte Kurvendiskussion von e- bzw. ln-Funktionen.
(bzw. Abwandlungen davon) die maximale Definitionsmenge finden kannst. Die korrekte Definitionsmenge ist Grundvoraussetzung für die Berechnung der jeweiligen Grenzwerte. Ohne Kenntnis der Definitionsmenge kannst du das Verhalten einer Funktion an den Rändern ihrer Definitionsmenge nicht untersuchen. Daher ist dieser Teil eine wichtige Grundlage für die nachfolgende Grenzwertberechnung und die gesamte Kurvendiskussion von e- bzw. ln-Funktionen.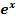 und / oder
und / oder 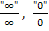 oder
oder 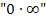 . Dabei kann man im Allgemeinen nicht sagen, was herauskommt, nur im jeweiligen Einzelfall. Wie du solche Grenzwerte dennoch schnell ermitteln und eventuell vorhandene Asymptotengleichungen daran ablesen kannst, wird besprochen in diesem Abschnitt.
. Dabei kann man im Allgemeinen nicht sagen, was herauskommt, nur im jeweiligen Einzelfall. Wie du solche Grenzwerte dennoch schnell ermitteln und eventuell vorhandene Asymptotengleichungen daran ablesen kannst, wird besprochen in diesem Abschnitt.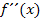 und ihre Anwendungen schon behandelt haben!) Wie man speziell bei e- oder ln-Funktionen das Krümmungsverhalten untersucht und die Wendepunkte berechnet, wird in diesem Teil erklärt. Es wird auch gezeigt, wie du die Gleichung einer Wendetangente aufstellst.
und ihre Anwendungen schon behandelt haben!) Wie man speziell bei e- oder ln-Funktionen das Krümmungsverhalten untersucht und die Wendepunkte berechnet, wird in diesem Teil erklärt. Es wird auch gezeigt, wie du die Gleichung einer Wendetangente aufstellst.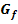 an den Rändern der Definitionsmenge, das Symmetrieverhalten, Schnittpunkte mit den Koordinatenachsen, Extrema und Monotonie, Wendepunkte und Krümmungsverhalten, bis zum Graph
an den Rändern der Definitionsmenge, das Symmetrieverhalten, Schnittpunkte mit den Koordinatenachsen, Extrema und Monotonie, Wendepunkte und Krümmungsverhalten, bis zum Graph 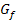 der Funktion! Hier wird das Wichtigste dazu gezeigt. Auch die Integralfunktion und Stammfunktion einer e- bzw. ln-Funktion wird kurz behandelt.
der Funktion! Hier wird das Wichtigste dazu gezeigt. Auch die Integralfunktion und Stammfunktion einer e- bzw. ln-Funktion wird kurz behandelt.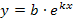 (mit
(mit 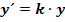 wird durch
wird durch 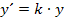 anschaulich bedeutet und wie Aufgaben dazu aussehen können, erfährst du in diesem Teil.
anschaulich bedeutet und wie Aufgaben dazu aussehen können, erfährst du in diesem Teil.