Die ln-Funktion:y = lnx
Sie werden immer negativer, d.h. immer kleiner, je näher man an x = 0 heran geht. Für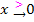 
geht die Funktion 
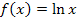gegen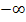 
, weil der Graph dort steil nach unten schießt. Somit gilt:
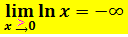
Erläuterung:Auf der y-Achse liegen die kleinen Zahlen ganz weit unten und die großen ganz weit oben. Beispielsweise ist die Zahl y = -5 kleiner als y = -4;die -5 liegt weiter unten auf der y-Achse als die -4.
Wenn dir das unlogisch vorkommt, denke einfach an die Temperatur:-5°C ist doch auch eine niedrigere Temperatur als -4°C. Auf der y-Achse liegt 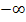daher ganz weit unten und umgekehrt 
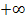ganz weit oben. Deshalb geht eine Funktion gegen 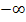, wenn ihr Graph steil nach unten schießt.
Nun zum zweiten Grenzwert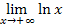 
. Was kommt dabei heraus? Überlege erst mal selbst!
Am Graph musst du dabei in Gedanken ganz weit nach rechts gehen, weil auf der x-Achse die sehr großen Zahlen ganz weit rechts liegen und wir ja gerade den Grenzwert für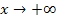 
ermitteln wollen. Dann fragst du dich, was mit den y-Koordinaten der Kurvenpunkte von 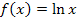passiert, wenn man x immer größer macht, also wenn man immer weiter nach rechts auf dem Graphen entlang geht. In der Abbildung ist zu erkennen, dass der Graph von 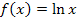für große x immer weiter ansteigt, zwar extrem langsam, aber er geht dennoch immer weiter nach oben. Die y-Koordinaten der Kurvenpunkte werden also immer größer, umso größer man x wählt:Die Funktion 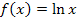geht für 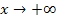ebenfalls gegen 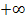, wenn auch sehr langsam. Daher gilt:
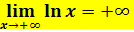
Ableitung und Monotonie der ln-Funktion:
Wegen x >0 (vergleiche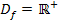 
) gilt:
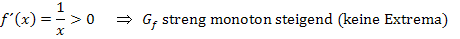
Dass der Graph der ln-Funktion streng monoton steigend ist und keine Extrema besitzt, erkennt man natürlich auch direkt an der Abb. oben!
Stammfunktion der ln-Funktion:
Um eine Stammfunktion F(x) von 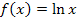zu finden, muss man die ln-Funktion integrieren, was jedoch nicht so einfach ist. Daher musst du die ln-Funktion nicht selbst integrieren können;du darfst einfach die Formel aus der Formelsammlung bzw. Merkhilfe für G8 verwenden.
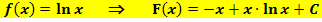
Wir begnügen uns an dieser Stelle mit dem rechnerischen Nachweis der Korrektheit dieser Stammfunktion, indem wir die Gültigkeit von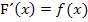 
zeigen. Wir leiten also die Stammfunktion 
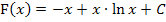ab und zeigen, dass dabei tatsächlich die Funktion 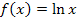herauskommt. Um 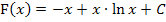abzuleiten, brauchen wir unter anderem die Produktregel, weil 
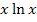ein Produkt ist, das in beiden Faktoren die Variable x enthält.
