Definitionsmenge ermitteln bei e- und ln- Funktionen
Empfehlung:Das teilweise graphische Verfahren zu Lösung von quadratischen Ungleichungen, das soeben vorgestellt wurde, geht etwas einfacher als das zuerst erklärte rein rechnerische Verfahren. Das graphische Verfahren ist absolut ausreichend, um auch in Prüfungen volle Punktzahl zu erhalten. Also besser das teils graphische Verfahren für quadratische Ungleichungen anwenden! Du musst allerdings wirklich eine kleine Skizze anfertigen, nicht nur im Kopf überlegen. Sonst kann der Lehrer deinen Lösungsweg nicht nachvollziehen.
Zu 2e.)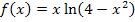 
Gesucht: 
Das Argument des natürlichen Logarithmus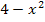 
muss positiv sein. Es ist daher folgende Ungleichung zu lösen:
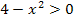
Es handelt sich wie schon in Teilaufgabe 2d. um eine quadratische Ungleichung, also um eine Ungleichung mit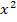 
. Wie man solche Ungleichungen lösen kann, wurde schon bei Teilaufgabe 2d. ausführlich erläutert. Wir können die beiden in 2d. beschriebenen Verfahren anwenden, um die Ungleichung 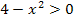zu lösen. Welchen Lösungsweg du nehmen willst, bleibt dir selbst überlassen. Im Folgenden werden noch einmal beide Varianten gezeigt.
1. Methode die quadratische Ungleichung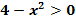 
zu lösen:Rein rechnerischer Weg
Wir faktorisieren die linke Seite der Ungleichung, d.h. wir formen die vorliegende Differenz 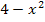in ein Produkt um. Hier geht das sehr leicht, weil sich die dritte binomische Formel anwenden lässt. (Wie man generell faktorisieren kann, wird erklärt bei:Faktorisierter Funktionsterm)
Zur Erinnerung hier die dritte binomische Formel: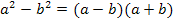 
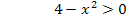
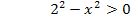
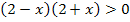
Nun liegt eine Ungleichung der Form:„Produkt >0“ vor. Bekanntlich ergibt Plus mal Plus wieder Plus, aber auch Minus mal Minus ergibt Plus. Daher ist ein Produkt größer Null, also positiv, wenn entweder beide Faktoren positiv sind oder beide negativ.
1. Fall:Beide Faktoren positiv oder 2. Fall:Beide Faktoren negativ
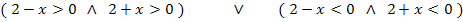
Mit Hilfe eines Zahlenstrahls lässt sich leicht herausfinden, welche Zahlenbereiche jeweils beide Ungleichungen des 1. Falls zugleich bzw. beide Ungleichungen des 2. Falls zugleich erfüllen. Wir suchen also beim 1. Fall nach der Schnittmenge der beiden Mengen x <2 und x >-2 und beim 2. Fall nach der Schnittmenge der beiden Mengen x >2 und x <-2.
Zum 1. Fall: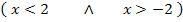 
Wir markieren den Zahlenbereich, der zur ersten Ungleichung x <2 gehört, zum Beispiel blau. Den Zahlenbereich, der zur zweiten Ungleichung x >-2 gehört, markieren wir in einer anderen Farbe, zum Beispiel rosa.
