Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Du kannst die Ortskurve der Hochpunkte mit einigen ausgewählten Graphen der Schar in der nachfolgenden Abbildung sehen.
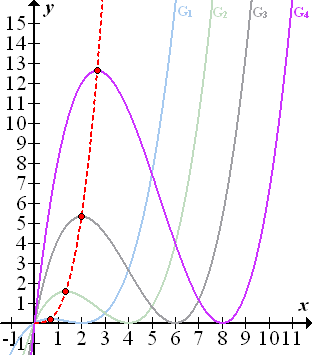
Abb.:Einige Graphen der Schar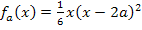 
zusammen mit der Ortskurve der relativen Hochpunkte 
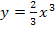(rot gestrichelt)
Anzumerken bleibt, dass wegen a >0 die x-Koordinaten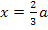 
der Hochpunkte ebenfalls immer positiv sind. Daher gilt die Ortskurve nur für x >0. Der Graph der Ortskurve darf deswegen nur rechts von der y-Achse gezeichnet werden.
Zum Einführungsbeispiel 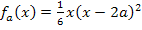mit a >0
b.) Gesucht:Ortskurve der Wendepunkte (d.h. es ist die Gleichung derjenigen Kurve gesucht, auf der alle Wendepunkte der Schar liegen.)
Lösung (nach der 1. Methode)
1. Schritt:Berechnung der x- und y-Koordinate des Wendepunktes in Abhängigkeit von a
Die erste und zweite Ableitung haben wir bei der Ermittlung der Ortskurve der Hochpunkte bereits gebildet.
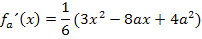
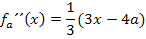
Um die x-Koordinate des Wendepunktes zu ermitteln, setzen wir die zweite Ableitung gleich Null. (Bei einem Wendepunkt ist die Krümmung des Graphen schließlich immer gleich Null und die Krümmung entspricht ja der zweiten Ableitung der Funktion.)
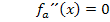
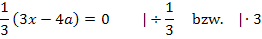
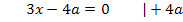
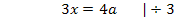
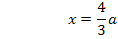
Vermutlich liegt bei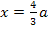 
eine Wendestelle der Schar vor. Das müssen wir aber erst noch nachweisen. Entweder zeigt man, dass sich an dieser Stelle das Vorzeichen der zweiten Ableitung wirklich ändert, oder wir weisen nach, dass die dritte Ableitung an dieser Stelle ungleich Null ist. (Siehe auch:Wendepunkte mit der dritten Ableitung nachweisen) Auf beide Arten lässt sich nachweisen, dass wirklich ganz sicher ein Wendepunkt und nicht bloßein Flachpunkt der Schar vorliegt. Es kann sein, dass ihr im Unterricht die dritte Ableitung nicht durchgenommen habt. Dann musst du den Vorzeichenwechsel der zweiten Ableitung nachweisen. Das ist hier aber ziemlich aufwendig. Sehr viel einfacher geht es mit der dritten Ableitung. Man muss nur die dritte Ableitung 
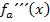bilden und für jedes darin vorkommende x die vorher ermittelte x-Koordinate des vermutlichen Wendepunktes einsetzen. Kommt dabei irgendeine Zahl ungleich Null heraus, weißman, dass tatsächlich ein Wendepunkt vorliegt. Deshalb verwenden wir hier den Nachweis mit der dritten Ableitung.
Nachweis des WEP:
Wir leiten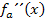 
noch einmal ab:
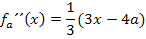
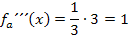
Eigentlich müsste jetzt die oben ermittelte x-Koordinate 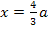in die dritte Ableitung 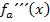für x eingesetzt werden. Da hier aber bei 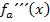gar kein x mehr vorkommt, braucht man die x-Koordinate auch nicht wirklich einzusetzen. Es kommt bei 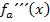sowieso für jedes beliebige x das Ergebnis 1 heraus und die Zahl 1 ist auf jeden Fall ungleich Null.
