Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
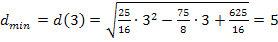
6. Schritt:Randpunktuntersuchung
Entfällt in diesem Beispiel, da es bei der Ersatz-Zielfunktion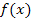 
und somit auch bei der Zielfunktion 
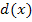selbst nur ein einziges Extremum gibt.
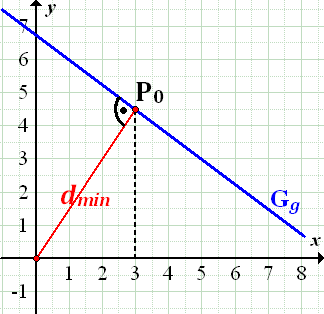
Damit ist die Aufgabe gelöst. Der Geradenpunkt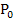 
, der vom Ursprung den kürzesten Abstand 
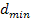besitzt, hat die Koordinaten 
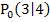. Der minimale Abstand von 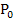zum Ursprung beträgt 
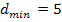LE (Längeneinheiten).
Hinweis:Die Gerade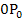 
steht auf der Gerade 
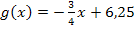senkrecht. Der Abstand eines Punktes zu einer Geraden ist schließlich die kürzeste Entfernung dieses Punktes zu der Geraden und dies ist natürlich das Lot (die senkrechte Gerade) von diesem Punkt auf die Gerade. Der Ursprung 0 hat von der Gerade 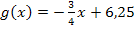somit den Abstand 5 LE. Der Punkt 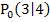ist der Lotfußpunkt.
3. Bsp.:
Wir betrachten die Funktion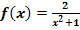 
in ihrer maximalen Definitionsmenge 
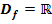. Auf der Funktion 
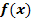liegen die Punkte 
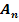und 
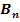, wobei 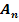im I. Quadranten und 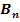im II. Quadranten liegt. Die Punkte 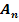und 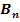bilden zusammen mit dem Ursprung 0 ein gleichschenkliges Dreieck mit der Spitze im Ursprung. Das Dreieck 
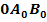hat den größtmöglichen Flächeninhalt. Berechne die Koordinaten von 
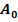und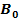 
! Wie großist dieser maximale Flächeninhalt?
Lösung:
Bezeichnung der Variablen festlegen:
Vorweg zeichnen wir uns am besten eine Skizze, die den Sachverhalt anschaulich darstellt. Ob du einfach eine Wertetabelle machst, um den Graphen zu skizzieren, oder eine Minikurvendiskussion, bleibt dir selbst überlassen. Was man an der Funktionsgleichung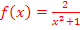 
ohne lange Rechnung erkennen kann
Wenn ein Punkt auf einer bestimmten Funktion 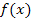liegt, kann man an Stelle der y-Koordinate des Punktes einfach die Funktionsgleichung von 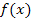schreiben. Die Punkte 
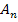liegen auf dem Graph 
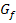mit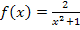 
.
Somit gilt: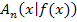 
bzw. 
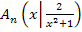mit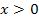 
.
Wir haben also festgelegt, dass die x-Koordinate von 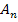mit x bezeichnet wird, und nicht etwa die von 
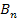. Wir rechnen also in Abhängigkeit von der x-Koordinate der Punkte 
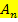. Das ist geschickter, als wenn wir die x-Koordinate der Punkte 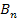mit x bezeichnet hätten, denn dann wäre x negativ gewesen. Da sich 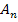laut Angabe im I. Quadranten befindet, muss die x-Koordinate x von 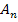positiv sein. ( 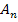liegt schließlich irgendwo rechts von der y-Achse.) Deshalb gilt: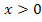 
Die x-Koordinaten der Punkte 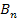, die im II. Quadranten liegen, sind dagegen negativ. ( 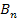liegt schließlich irgendwo links von der y-Achse, symmetrisch zu .)
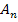Wir zeichnen als Beispiel das Dreieck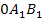 
für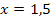 
.
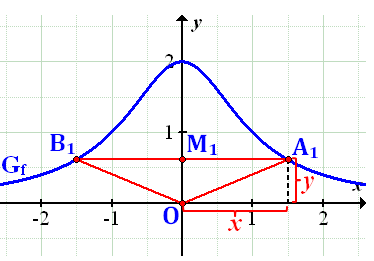
Abb.:Graph 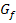der Funktion 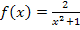mit Dreieck 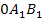(rot eingezeichnet)
