Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

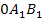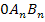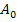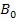Das rot eingezeichnete Dreieck stellt ein beliebiges Beispiel der Dreiecke dar. Es handelt sich mit größter Wahrscheinlichkeit noch nicht um das flächengrößte Dreieck. Wenn es tatsächlich das flächengrößte Dreieck ist, wäre das reiner Zufall. Die Koordinaten der Eckpunkte und des flächengrößten Dreiecks  müssen wir schließlich erst ermitteln. Du könntest nun zusätzlich weitere Beispieldreiecke 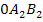und 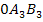einzeichnen. Das macht die Zeichnung aber nur unübersichtlicher. Daher verzichten wir hier darauf.

1. Schritt:Nebenbedingung aufschreiben

Genau genommen ist hier die Funktionsgleichung 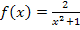die Nebenbedingung, weil die Punkte 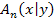auf der Funktion 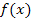liegen sollen.

Wir haben vorher die Nebenbedingung bereits verwendet, als wir 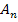in der Form 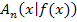bzw. 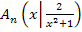geschrieben haben. Wir haben einfach y durch 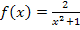ersetzt. Man kann die Nebenbedingung entweder gleich zu Beginn in 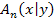einsetzten – das spätere Einsetzten der Nebenbedingung in die Hauptbedingung entfällt dann – oder man stellt die Hauptbedingung erst mit x und y auf, und setzt danach erst die Nebenbedingung für y ein, so wie wir das bisher bei den anderen Beispielen immer gemacht haben. Damit du nicht durcheinander kommst, bleiben wir bei dieser Methode. Wenn du dich auch für den anderen Weg interessierst, siehe:Alternativweg zum 3. Bsp.

2. Schritt:Hauptbedingung aufstellen

Der Flächeninhalt des Dreiecks soll maximal werden. Daher überlegen wir uns erst einmal, wie man den Flächeninhalt eines Dreiecks berechnet.

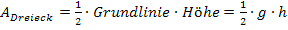
Als Grundlinie verwenden wir die Seite 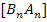. Sie hat eine Länge von .

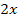Die zugehörige Höhe 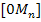hat die Länge y.

Somit gilt für den Flächeninhalt der Dreiecke :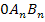

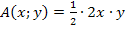
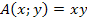
Dies ist die Hauptbedingung.

3. Schritt:Nebenbedingung nach einer Variablen auflösen und in die Hauptbedingung einsetzten:

Die Nebenbedingung 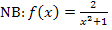ist im Prinzip schon nach y aufgelöst, da 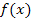nur eine andere Schreibweise für y ist. Der Ausdruck 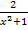braucht nur noch für y in die Hauptbedingung 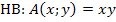eingesetzt zu werden. So bekommen wir die Zielfunktion. Sie enthält dann nur noch die Variable x.

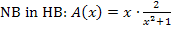
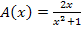
Dies ist die Zielfunktion.

4. Schritt:Definitionsmenge der Zielfunktion angeben

Da sich 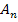laut Angabe im I. Quadranten befindet, muss die x-Koordinate x von 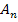positiv sein. ( 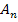liegt schließlich irgendwo rechts von der y-Achse.)  Deshalb gilt: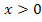

Somit ist die Definitionsmenge: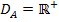

5. Schritt:Extrema der Zielfunktion 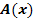berechnen

Hier noch einmal die Zielfunktion: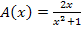

Um ihre Extrema berechnen zu können, bilden wir die erste Ableitung.

---