Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

)

Zweite Ableitungbilden: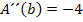

Eigentlich müsste nun 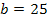in die zweite Ableitung eingesetzt werden. Da hier allerdings kein b mehr in der zweiten Ableitung vorkommt, kann man 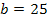gar nicht in die zweite Ableitung einsetzen. Die Krümmung ist einfach immer 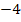, egal an welcher Stelle, also auch für 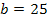. Daher gilt:

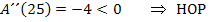
2. Methode:Untersuchung des Monotonieverhaltens

Zuerst zeichnen wir eine Tabelle der folgenden Form.

b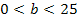
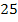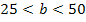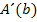		0

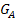Beachte dabei die Definitionsmenge 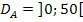! Das linke Intervall beginnt daher nicht bei 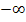, sondern erst bei 0. Das rechte Intervall geht nur bis 50 und nicht bis .

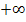Nun überlegen wir uns die Vorzeichen der Ableitung 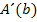in den beiden Intervallen. Denk dir einfach jeweils irgendeine konkrete Zahl aus einem der Bereiche, setze sie in die Ableitung 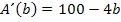ein und bestimme das Vorzeichen des Ergebnisses! Mit dem anderen Bereich geht es entsprechend.

Zum Beispiel:

Aus dem Bereich 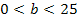nehmen wir mal die Zahl 10. Setzt man 10 in die Ableitung ein, ergibt sich:

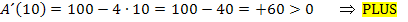
Das Plus-Zeichen tragen wir nun in die Tabelle ein.

b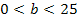
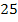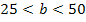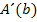		0

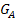Aus dem Bereich 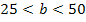nehmen wir mal die Zahl 30. Setzt man 30 in die Ableitung ein, ergibt sich:

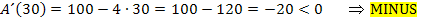
Das Minus-Zeichen tragen wir auch noch in die Tabelle ein.

b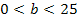
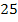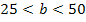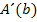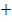		0

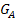Wir müssen jetzt überlegen, was die Vorzeichen der Ableitung mit dem Verlauf des Graphen zu tun haben. Du weißt sicher, dass eine Funktion streng monoton steigend ist, wo ihre Ableitung positiv ist, und umgekehrt streng monoton fallend, wo die Ableitung negativ ist.

b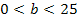
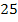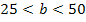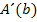		0
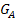	streng monoton steigend	HOP	streng monoton fallend

Unsere Zielfunktion ist somit zuerst steigend, dann fallend. An der Stelle 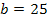liegt daher ein Hochpunkt der Zielfunktion vor. Es handelt sich, wie gesagt, um einen absoluten Hochpunkt, da die Funktion ihre Monotonie nur an dieser Stelle ändert und somit kein anderer Kurvenpunkt höher liegen kann. Die y-Koordinate des Hochpunktes ist somit der absolut höchste Funktionswert, den die Funktion 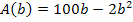annehmen kann. D.h. die y-Koordinate des Hochpunktes entspricht dem absolut größten Flächeninhalt 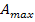der Koppel.

Um 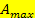zu berechnen, muss man also nur 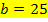in die Zielfunktion 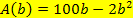einsetzen.

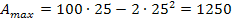
Der maximale Flächeninhalt der Koppel beträgt 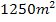. Er ergibt sich bei einer Breite der Koppel von .

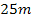Die zugehörige Länge lässt sich leicht berechnen, indem man die Breite 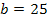in die Gleichung 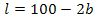einsetzt.

---