Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
Im Folgenden sollen die Begriffe „Differenzenquotient“ und „Differenzialquotient“ eingeführt und ihre unterschiedliche Bedeutung für eine Funktion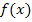 
erläutert werden. Wir nähern uns der Thematik erst einmal von der „klassischen Seite“. Das heißt, dass die Begriffe als Sekanten- bzw. Tangentensteigung gedeutet werden. So war das früher im G9 üblich und wird auch im G8 und auf der FOS/BOS noch von vielen Lehrern gemacht. Vor allem im G8 führen allerdings einige Lehrer über die „mittlere Änderungsrate“ bzw. „lokale Änderungsrate“ des Funktionswerts zu den Begriffen des „Differenzenquotienten“ bzw. „Differenzialquotienten“ hin. Um auch den Schülern zu helfen, deren Lehrer mit den Änderungsraten das Thema einleiten, wird im unteren Teil (ab dem 6. Bsp.) noch einmal von dieser Seite an das Thema herangeführt. Wir beginnen hier jedoch mit dem Problem der Berechnung der Tangentensteigung.
Schon einmal vorweg genommen:
Der „Differenzenquotient“ entspricht sowohl der Sekantensteigung als auch der mittleren Änderungsrate.
Der „Differenzialquotient“ entspricht sowohl der Tangentensteigung als auch der lokalen Änderungsrate.
Was ist denn nun überhaupt der „Differenzenquotient“ oder der „Differenzialquotient“? Wie rechnet man das jeweils aus? Um dies zu erklären, müssen wir etwas weiter ausholen.
Hinführung zur Problematik bei der Berechnung der Tangentensteigung
Es ist eine Funktion durch ihre Funktionsgleichung gegeben, beispielweise die Normalparabel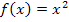 
. Es kann sich natürlich auch um eine wesentlich schwierigere Funktion handeln. Mit Hilfe einer Wertetabelle könnte der Funktionsgraph auch dann leicht gezeichnet werden, wenn die Funktion komplizierter ist. Den Graph der Funktion zu zeichnen, stellt also kein großartiges Problem dar. Es soll nun jedoch zusätzlich in einem bestimmten Kurvenpunkt die Tangente an den Graph gelegt werden. Wir wissen, dass eine Tangente den Funktionsgraph in genau einem Kurvenpunkt berührt, aber in der näheren Umgebung nicht schneiden darf. Beim Zeichnen der Tangente ergibt sich das Problem, dass wir eigentlich zwei Punkte bräuchten, um sie eindeutig zeichnen zu können, wir aber nur einen Punkt gegeben haben, nämlich den Kurvenpunkt, in dem die Tangente den Graph berührt. Man könnte jetzt mit dem Geodreieck so lange herumprobieren, bis sich ungefähr die Tangente ergibt. Aus der Zeichnung könnte dann die Tangentensteigung abgelesen werden. Das bezeichnet man als „graphisches Differenzieren“. Mit „Differenzieren“ ist im Prinzip immer gemeint „Steigung einer Kurve ermitteln“. Doch das graphische Differenzieren ist meist ziemlich ungenau, weil man eine Tangente niemals ganz exakt einzeichnen kann. (Siehe auch:Genauere Erklarungen zum graphischen Differenzieren)
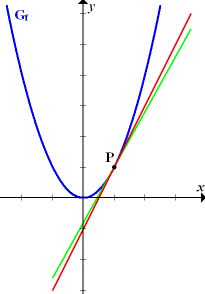
Abb.:Graph einer Parabel mit zwei Geraden, welche die Tangente im Punkt P sein könnten
Es könnte sich in der oben gezeigten Abbildung beispielsweise bei der roten Gerade um die Tangente im Punkt P handeln, aber auch bei der grünen Geraden. Das lässt sich so einfach nicht feststellen. (Übrigens:Die rote Gerade ist tatsächlich die Tangente im Punkt P!)
