Delta-x-Methode

Mit 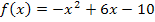ergibt sich:

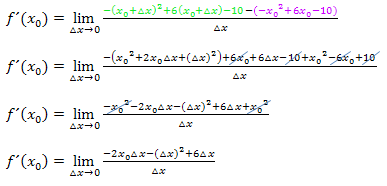
Jetzt lässt sich 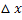im Zähler ausklammern.

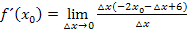
Nach dem Ausklammern liegt im Zähler ein Produkt vor. Wir dürfen jetzt kürzen. Das ergibt:

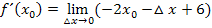
Wir führen den Grenzübergang durch, d.h. wir setzen gleich Null:

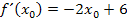
Der Term 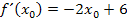entspricht der Steigung der Funktion 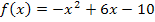in einem allgemeinen festen Kurvenpunkt ( .

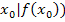Nun können wir schnell jeweils die Steigung der Funktion in den angegebenen Punkten P(2|f(2)), Q(3|f(3)) und R(4|f(4)) berechnen, indem wir in 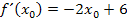nacheinander die Werte 2, 3 und 4 für 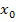einsetzen:

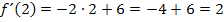
Das ist die Steigung der Funktion im Punkt P(2|f(2)).

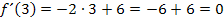
Das ist die Steigung der Funktion im Punkt P(3|f(3)).

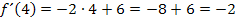
Das ist die Steigung der Funktion im Punkt P(4|f(4)).

Die Aufgabe ist damit gelöst.

Betrachte trotzdem noch einmal den Ausdruck 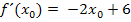! Wenn man statt 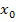einfach x schreibt, erhalten wir die sogenannte Ableitungsfunktion 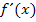der Funktion .

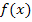Für die Funktion 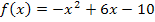gilt also:

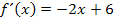
Wenn du das Ergebnis von 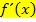schnell im Kopf überprüfen willst, musst du nur folgendes machen:Bei jeder x-Potenz von 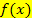den Exponenten nach vorne ziehen und mit der Zahl davor multiplizieren, außerdem die Zahl 1 vom Exponenten abziehen. Zahlen ganz ohne x fallen dann ganz weg, weil man sich zu einer Zahl ohne x einfach 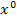dazu denken kann und Null mit etwas multipliziert ergibt Null, fällt also weg. So kannst du 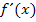ganz leicht im Kopf ermitteln.

Kontrolle:

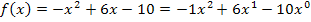
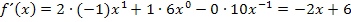
(Zur Erinnerung: )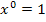

Super, das Ergebnis stimmt mit dem überein, das wir oben mit viel Mühe mit dem Differenzialquotienten gebildet haben. Es stimmt somit alles. (Ausführlichere Erläuterungen zu der Schnellmethode, mit der wir soeben 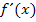im Kopf gebildet haben, findest du im Abschnitt:Einfache AbleitungsregelnLeider darfst du dieses Verfahren offiziell erst später anwenden.)

Die Ableitungsfunktion 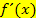beschreibt die relative Veränderung der Funktionswerte von .

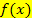Je stärker sich die Funktionswerte von 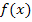im Vergleich zu x ändern, desto steiler verläuft der Graph der Funktion 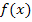. Umgekehrt verläuft der Graph von 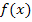umso flacher, je weniger sich die Funktionswerte relativ zu x ändern. Die relative Veränderung 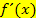der Funktionswerte entspricht daher dem Steigungs- bzw. Monotonieverhalten der Funktion 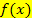. Das Berechnen der Ableitungsfunktion 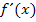bezeichnet man als globales Differenzieren.

Um mit Hilfe von 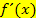die Steigung von 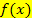in einem bestimmten Kurvenpunkt 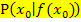zu berechnen, muss dann bloßnoch die gegebene x-Koordinate 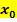des Kurvenpunktes in die Ableitungsfunktion eingesetzt werden und schon hat man die Steigung 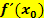der Funktion 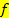in diesem Kurvenpunkt. Das Berechnen der Ableitung 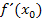an einer bestimmten Stelle 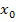nennt man lokales Differenzieren.

---