Variante 3
Wir wollen die Steigung einer Funktion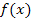 
in einem gegebenen Punkt 
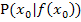berechnen, also die Steigung der Tangente an 
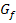in diesem Punkt.
Wir bleiben vorerst bei unserem Einführungsbeispiel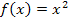 
mit dem Punkt 
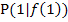. Wie kann man nun die Tangentensteigung im Punkt P berechnen?
Zusätzlich zum gegebenen, festen Kurvenpunkt 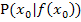verwenden wir wieder einen zweiten Kurvenpunkt H als Hilfspunkt. Da auch H auf der Funktion 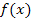liegt, kann man allgemein 
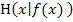schreiben, wobei gelten soll 
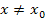. (Mit 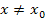ist gemeint, dass H und P verschiedene x-Koordinaten haben sollen, also dass H wirklich ein anderer Punkt ist als P.) Durch die beiden Kurvenpunkte P und H ist daher eine Gerade festgelegt. Sie schneidet den Graph der Funktion 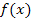natürlich genau in den Punkten P und H. Daher ist die Gerade PH eine Sekante des Graphen. Betrachte dazu die folgende Abbildung!
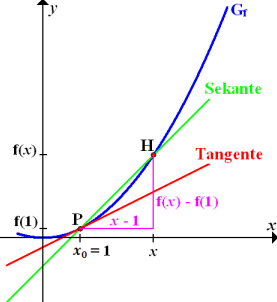
Abb.:Zur Berechnung der Tangentensteigung zu 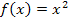im Punkt 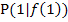. Der Hilfspunkt H wird immer näher an den festen Punkt P heran geschoben, d.h. x geht gegen 1. So wird aus der Sekantensteigung letztendlich die Tangentensteigung.
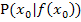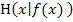Mit Hilfe der beiden Punkte und sowie der Formel 
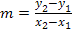lässt sich die Sekantensteigung 
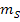berechnen.
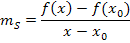
Dieser Ausdruck ist der Differenzenquotient.
Beachte dabei den Unterschied zwischen x und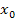 
! 
steht für die x-Koordinate des angegebenen Punktes P, also für eine feste Zahl. In unserem Einführungsbeispiel hat der Punkt 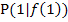die x-Koordinate 1, daher ist hier 
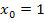. In einfacheren Worten: ist grundsätzlich die x-Koordinate des angegebenen Punktes P. Dagegen ist x eine beliebige, variable Zahl, die nur nicht exakt mit zusammenfallen darf, denn es muss gelten: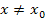
Vom Differenzenquotienten, der nur die Sekantensteigung angibt, kommt man zum Differenzialquotienten, welcher letztendlich die gesuchte Tangentensteigung im Punkt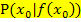 
ergibt, indem man den Hilfspunkt 
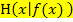beliebig nah an den gegebenen festen Kurvenpunkt 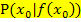heranschiebt. Dadurch wird aus der Sekante letztendlich die Tangente im Punkt 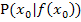und aus der Sekantensteigung durch die Annäherung von x an die gesuchte Tangentensteigung. Dieses Heranschieben von x an wird mathematisch durch die Schreibweise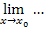 
(sprich:„Limes x gegen x Null“ ausgedrückt. So erhalten wir für die Tangentensteigung im Punkt :
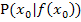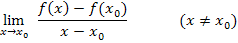
Dieser Ausdruck heißt Differenzialquotient der Funktion 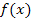an der Stelle . Er beschreibt die Steigung der Tangente an die Funktion 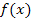im Punkt .
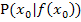Da die Tangentensteigung der Steigung der Funktion in diesem Punkt entspricht, lässt sich mit Hilfe des Differenzialquotienten auch die Steigung der Funktion im Punkt 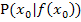berechnen.
Die Steigung einer Funktion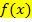 
an der Stelle 
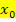wird als erste Ableitung 
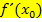, kurz Ableitung, der Funktion an der Stelle 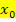bezeichnet.
Daher gilt für die Tangentensteigung bzw. für die Steigung der Funktion an der Stelle :
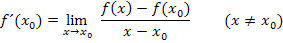
Mit Hilfe der folgenden Abbildung kannst du dir den Sachverhalt hoffentlich einigermaßen vorstellen.
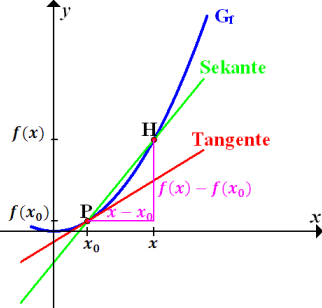
Abb.:Graph einer Funktion 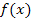mit den Kurvenpunkten P und H einschließlich der Tangente in P und der Sekante PH
