Stetigkeit und Differenzierbarkeit
Leider steht bei der Funktion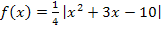 
der Betrag nicht ganz außen. Der Bruch 
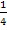steht dummerweise außerhalb. Weil 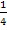aber positiv ist, kann es allerdings in den Betrag hinein geschrieben werden und es gilt:
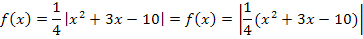
Nun lässt du den Betrages vorerst mal weg, dann erhältst du die Funktion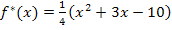 
. Der Graph dieser Funktion ist eine breitere nach oben geöffnete Parabel mit den Nullstellen bei 
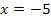und 
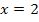. Den Betrag dieser Funktion bildet man graphisch, wie oben schon erklärt, indem man den Teil der Parabel, der unterhalb der x-Achse liegt, an der x-Achse spiegelt. Den anderen Teil der Parabel lässt man wie er ist. Du musst also nur den unterhalb der x-Achse liegenden Teil der Parabel 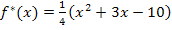nach oben klappen, um den Graph von 
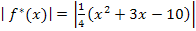also den von 
zu erhalten.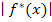 
entspricht schließlich genau unserer Funktion .
Das bedeutet also, dass man einfach den Graph der Parabel 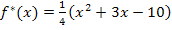zeichnen und den Teil, der unterhalb der x-Achse liegt, nach oben klappen muss, um den Graph von 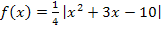zu erhalten. Die betragsfreie Form erhält man dann ganz einfach, indem man sich überlegt, in welchen Bereichen die Parabel gespiegelt wurde bzw. in welchen nicht. Bei dem Bereich bzw. den Bereichen, wo an der x-Achse gespiegelt wurde, muss man entsprechend ein Minus zum Funktionsterm dazu schreiben, wenn man den Betrag auflöst. Bei denjenigen Bereichen, die nicht gespiegelt wurden, kann man den Betrag einfach durch eine Klammer ersetzen.
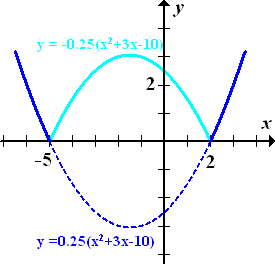
Zur Abbildung:Die dunkelblaue, nach oben geöffnete Parabel hat die Gleichung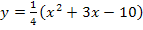 
sie gilt nur für 
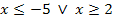, weil sie in diesem Bereich schon oberhalb der x-Achse liegt und nicht gespiegelt werden musste. Die hellblaue, nach unten geöffnete Parabel hat die Gleichung 
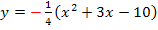sie gilt nur für 
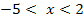, weil die dunkelblaue Parabel in diesem Bereich unterhalb der x-Achse liegen würde (gestrichelter Teil);in diesem Bereich musste also gespiegelt werden. Deshalb muss das Minus bei der Funktionsgleichung dazu geschrieben werden.
Es gibt bei dieser Funktion zwei Nahtstellen;die eine liegt bei 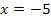, die andere bei 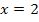. Wir müssen sie jeweils einzeln auf Differenzierbarkeit untersuchen. Die vorherige Überprüfung der Stetigkeit entfällt erfreulicherweise, da in der Aufgabenstellung bereits erwähnt ist, dass die Funktion in ihrer gesamten Definitionsmenge stetig ist, also auch an den Stellen 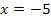und 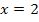. Aus unseren Überlegungen bezüglich des Graphen ist an sich bereits klar, dass die Funktion 
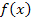an beiden Stellen einen Knick hat und somit dort nicht differenzierbar sein kann. Dennoch muss dies rechnerisch gezeigt werden.
