Stetigkeit und Differenzierbarkeit
Dadurch ergibt sich der Graph von 
.
Du möchtest noch wissen, warum das so geht? Ganz einfach:Wie du weißt, macht der Betrag alle negativen Zahlen positiv. Bei positiven Zahlen ändert der Betrag gar nichts. Nur wo die Parabel unterhalb der x-Achse verläuft, sind die y-Werte negativ. Wegen des Betrages müssen sie aber positiv gemacht werden. Das erreicht man durch das Spiegeln an der x-Achse. Wo die Parabel schon oberhalb der x-Achse liegt, sind die Funktionswerte positiv. Der Betrag verändert in diesem Bereich nichts mehr.
Durch die beschriebene Spiegelung des Teils bzw. der Teile des Graphen, welche unterhalb der x-Achse verlaufen, ergeben sich die für Betragsfunktionen typischen Knicke. An den Knickstellen ist die Funktion natürlich nicht differenzierbar. Daher sind Betragsfunktionen in der Regel nicht in ihrer gesamten Definitionsmenge differenzierbar. Mehr zu Betragsfunktionen im Kapitel:Betragsfunktion, Signum-Funktion und Gaußsche Treppenfunktion
Manchmal wird bei nichtdifferenzierbaren Funktionen zusätzlich auch nach dem Knickwinkel gefragt. Wie man ihn berechnen kann, schauen wir uns im nächsten Beispiel an.
3. Bsp.:Knickwinkel gesucht
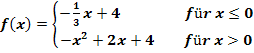
Zeige, dass die Funktion 
an der Stelle 
zwar stetig, aber nicht differenzierbar ist. Liegt an der Knickstelle ein Extremum vor? Berechne dann den Knickwinkel auf zwei Dezimalen gerundet!
Lösung:
Nachweis der Stetigkeit
1. Methode:
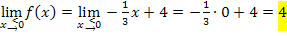
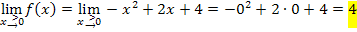
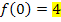
Es ergibt sich dreimal derselbe Wert. Es gilt also: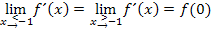 
Die Funktion ist somit stetig bei 
. Sie hat hier keine Sprungstelle. Das sollte schließlich gezeigt werden.
2. Methode:
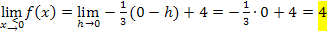
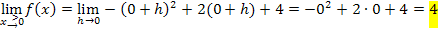
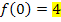
Wie auch schon mit der 1. Methode gezeigt, ergibt sich dreimal das gleiche Ergebnis. Die Funktion ist stetig bei .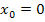
Untersuchung der Differenzierbarkeit
Hier noch einmal die Funktion: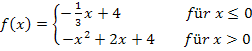 
1. Methode:
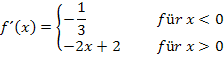
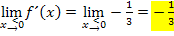
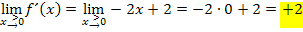
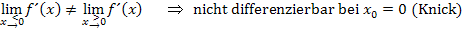
Da auch das Vorzeichen der Grenzwerte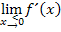 
und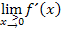 
unterschiedlich ist, liegt an der Knickstelle ein Extremum. Es handelt sich um einen Tiefpunkt, da der linksseitige Grenzwert der Ableitung negativ und der rechtsseitige positiv ist (Vorzeichenwechsel der Ableitung von Minus nach Plus), so dass die Funktion links von 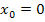fällt und direkt rechts davon steigt.
2. Methode:
Hier noch einmal die Funktion: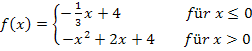
Linksseitige Annäherung an die Stelle :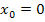
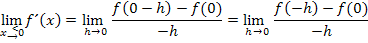
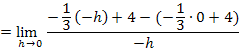
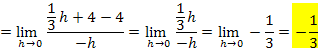
Rechtsseitige Annäherung an die Stelle :
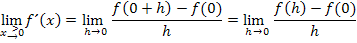
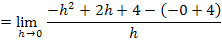
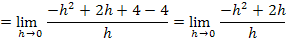
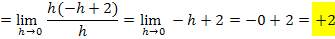
Wie schon bei der 1. Methode gezeigt, sind die Grenzwerte der Ableitung nicht gleich;die Funktion ist an der Stelle 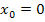nicht differenzierbar.
