Vorwort zur Differenzialrechnung
Die Differenzialrechnung ist ein Teilgebiet der Mathematik, welches sich mit Berechnungen an Funktionen beschäftigt, insbesondere der Untersuchung der Steigung (Monotonie/Monotonieverhalten) von kurvenförmigen Funktionsgraphen und ihrer Krümmung/Krümmungsverhalten. Um den Graph einer durch ihre Funktionsgleichung gegebenen Funktion f(x) auch ohne Wertetabelle zeichnen zu können, wird eine sogenannte Kurvendiskussion durchgeführt. Dabei werden neben den Schnittpunkten des Funktionsgraphen mit den Koordinatenachsen und dem Verhalten an den Rändern des Definitionsbereichs (Siehe:Definitionsmenge) unter anderem die Extrema und die Wendepunkte der Funktion berechnet. Dafür benötigt man die Differenzialrechnung, mit deren Mitteln sich die Steigung der unterschiedlichsten Funktionen, ihre Extrema und Wendepunkte berechnen lassen.
Die Steigung einer Funktion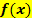 
entspricht immer der Steigung der Tangente von 
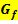an dieser Stelle. Das ist so definiert. Um die Steigung einer Funktion zu berechnen, muss also die jeweilige Tangentensteigung in dem entsprechenden Punkt des Graphen ermittelt werden. Das Berechnen der Tangentensteigung nennt man ableiten oder differenzieren. (Daher auch die Bezeichnung „Differenzialrechnung“.) Wird die Steigung einer Funktion in einem bestimmten Kurvenpunkt 
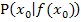ermittelt, spricht man lokalem Differenzieren. Wird dagegen die Steigung an einer allgemeinen Stelle x berechnet, spricht man von globalem Differenzieren. Mit Hilfe der Differenzialrechnung kann die Steigung der Tangente in jedem beliebigen Punkt P des Graphen ermittelt werden.
Die Steigung einer Funktion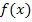 
, also ihre Tangentensteigung im jeweiligen Kurvenpunkt 
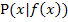, wird als erste Ableitung, kurz Ableitung, der Funktion 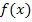bezeichnet. Man schreibt für die Ableitung 
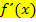. Sprich:„f Strich von x“
Die Ableitung 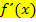entspricht also der Tangentensteigung der Funktion 
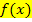. Vielleicht fragst du dich nun, warum man nicht einfach beispielsweise 
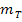für die Tangentensteigung als Abkürzung verwendet. Wahrscheinlich wäre 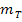für dich einleuchtender;m für Steigung und T für Tangente. Doch leider kann damit nicht ausgedrückt werden, an welcher Stelle x die Tangente an 
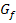gelegt wurde. Da sich die Steigung der Kurve 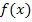und somit ihre Tangentensteigung aber von Punkt zu Punkt ändert, ist die Steigung einer Kurve keine konstante Zahl;die Tangentensteigung hängt vielmehr immer von der jeweiligen Stelle x ab. Genau dies drückt bei 
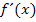das x in der Klammer aus. Die Ableitung 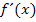– also die Steigung von 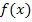– ist somit eine eigene Funktion;deshalb spricht man auch von der Ableitungsfunktion .
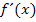Es ist zugegebenermaßen schwierig, sich die Steigung einer bestimmten Funktion 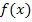als neue Funktion 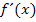vorzustellen, doch es gilt:Die Ableitungsfunktion 
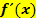ordnet jedem x die Steigung von 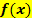an dieser Stelle zu;die y-Koordinate der Ableitungsfunktion 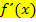entspricht somit der Steigung von 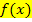an der jeweiligen Stelle.
Um die Ableitungsfunktion 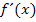zu ermitteln, gibt es bestimmte Regeln, die sogenannten Ableitungsregeln. Diese Regeln sind eigentlich gar nicht so schwer. Doch bevor wir sie anwenden dürfen, müssen wir uns erst mit einer ziemlich umständlichen Methode beschäftigen, die uns dann letztendlich zu den deutlich praktischeren Ableitungsregeln führt.
Wenn für dich das Thema „Differenzialrechnung“ ganz neu ist, solltest du dich unbedingt auch mit der Herleitung der Tangentensteigung aus der Sekantensteigung beschäftigen. (Das wird in der ersten Schulaufgabe zu diesem Thema sicher verlangt.) Die genaue Herleitung der Ableitung 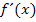wird gezeigt im Abschnitt: Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
Willst du dich allerdings nur schnell auf das Abitur oder auf eine spätere Schulaufgabe zu diesem Thema vorbereiten, kannst du diese Herleitung gleich überspringen und direkt zu den Ableitungsregeln übergehen. Die aufwendige Herleitung der Tangentensteigung mittels des sogenannten Differenzialquotienten brauchst du später bestimmt nicht mehr. Die Regeln, mit denen man später normalerweise immer ableitet, werden in den Abschnitten Einfache Ableitungsregelnund Weitere Ableitungsregelnan Hand vieler Beispiele ausführlich erklärt.
