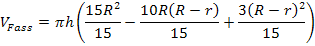3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Wegen der Achsensymmetrie zur y-Achse der Parabel und somit auch des Fasses gilt:
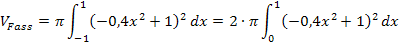
Mit der Zahl 0 als untere Integrationsgrenze erspart man sich nämlich später beim Einsetzen der Grenzen ein klein wenig Rechenaufwand. Daher entscheiden wir uns hier für diese Methode.
Um eine Stammfunktion zu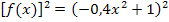 
bilden zu können, vereinfachen wir den Ausdruck in einer Nebenrechnung, indem wir die zweite binomische Formel 
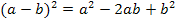anwenden. Dazu müssen wir die Reihenfolge innerhalb der Klammer umdrehen.
Nebenrechnung:
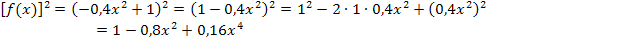
Jetzt können wir leicht mit Hilfe der Formel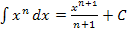 
eine Stammfunktion zu 
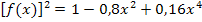finden und das Integral berechnen.
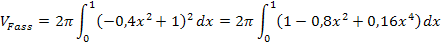
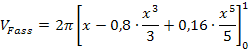
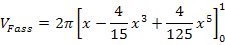
Einsetzen der Grenzen ergibt:
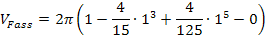
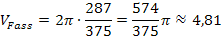
Zu 4c.)
Es soll allgemein gültig gezeigt werden, dass für das Volumen des Fasses, welches durch die Rotation der Parabel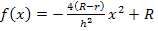 
mit x 
[-0,5h| 0,5h] um die x-Achse entsteht, die Formel 
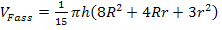gilt.
Wir setzen 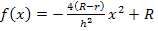zusammen mit den Grenzen a = -0,5h und b = 0,5h in die Formel für das Volumen von Rotationskörpern ein:
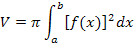
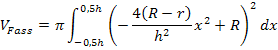
Wie schon in Teilaufgabe 4b.) nutzen wir die Tatsache, dass die Funktion 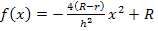achsensymmetrisch ist zur y-Achse.
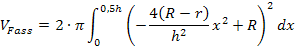
Um leichter eine Stammfunktion zu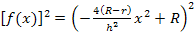 
bilden zu können, vereinfachen wir 
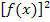ähnlich wie in Teilaufgabe 4b.) in einer Nebenrechnung mit Hilfe der zweiten binomischen Formel. Vorher müssen wir dazu allerdings noch die Reihenfolge in der Klammer vertauschen.
Nebenrechnung:
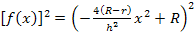
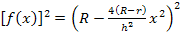
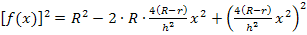
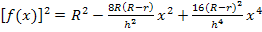
In der nun vorliegenden Form können wir schnell eine Stammfunktion dazu finden. Mit Hilfe der bekannten Integrationsregel 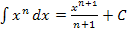lässt sich leicht eine Stammfunktion zu 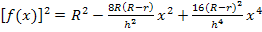berechnen. Die Buchstaben R, r und h sind dabei Konstanten, d.h. feste (wenn auch unbekannte) Zahlen, also keine Variablen. Einzige Variable ist x. Beim Integrieren nach dx darf man sich ausschließlich auf die Potenzen der Variablen, also auf die Potenzen von x konzentrieren. Nur bei den x-Potenzen erhöht man beim Integrieren nach dx die Potenz jeweils um 1 und dividiert anschließend durch den neuen Exponenten. Alle anderen Buchstaben müssen wie feste Zahlen behandelt werden. Nun können wir das gesuchte Integral allgemein berechnen. Versuche es doch erst einmal alleine, bevor du dir den Rest der Lösung anschaust! Die Rechnung ist zwar lang, aber eigentlich gar nicht so schwer.
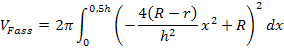
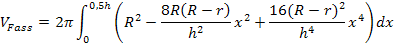
Integration:
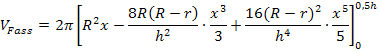
Einsetzen der Grenzen:
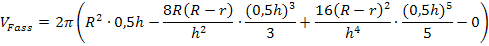
Vereinfachen:
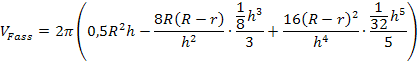
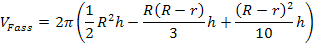
Der Faktor 2 wird in die Klammer hineinmultipliziert:
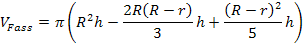
Ausklammern von h:
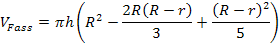
Hauptnenner in der Klammer bilden:
