3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen

Schauen wir uns einfach noch einmal die Formel des Volumens von Rotationkörpern an:

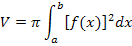
Wenn man dabei die untere Grenze a = 0 wählt, dann ergibt sich aus der allgemeinen Formel 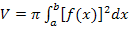der Sonderfall:

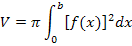
Die Ähnlichkeit zur Formel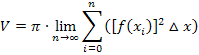

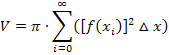
ist nicht zu übersehen.

Die Schreibweise dx beim Integral leitet sich ab von 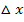(sprich:Delta x) in der Summenformel. Das Integral 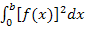entspricht der unendlichen Summe .

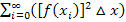Hinweis:Genau genommen darf man gar nicht von einer „unendlichen Summe“ sprechen;korrekt wäre „unendliche Reihe“. Eine unendliche Reihe ist zwar eine Summe mit unendlich vielen Gliedern, doch gelten für unendliche Reihen nicht die gleichen Rechengesetze wie für „normale“ Summen. Dies genauer zu erklären, würde allerdings zu weit führen. Unendliche Reihen braucht man erst im Studium der Mathematik, aber bestimmt nicht in der Schule.

Du fragst dich, wo in der Summenschreibweise die obere Integrationsgrenze b geblieben ist? Der Buchstabe b taucht in der Summenschreibweise nicht auf. Das liegt daran, dass man ähnlich der Streifenmethode bei der Herleitung der Fläche zwischen 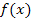und der x-Achse  den Bereich von 0 bis b auf der x-Achse in n Streifen (Zylinder) aufteilt, die jeweils die Streifenbreite (Höhe der Zylinder) 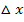haben. Somit gilt: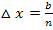

Das b steckt daher auch in der Formel mit der Summenschreibweise, nur versteckt im 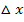. (Vergleiche auch:Die Streifenmethode)

Hoffentlich leuchten dir die beschriebenen Zusammenhänge soweit zumindest vom Prinzip her ein. Genau herleiten musst die Formel für das Volumen von Rotationskörpern sowieso nicht können.

Schauen wir uns lieber ein paar konkrete Beispiele an.

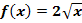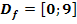1. Bsp.:Gegeben ist die Funktion mit . Ihr Graph 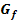rotiert um die x-Achse. Fertige eine Skizze, die den Graph 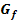und den Rotationskörper im Koordinatensystem zeigt, und berechne das Volumen des entstehenden Rotationskörpers!

Lösung:

Die Funktion 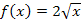ist eine um den Faktor 2 entlang der y-Achse gestreckte Wurzelfunktion. (Die Wurzelfunktion 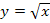ist die Umkehrfunktion der Normalparabel 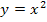mit x 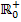. Den Graph der Wurzelfunktion erhält man daher durch Spiegelung des steigenden Astes der Normalparabel an der Winkelhalbierenden y = x.)  Du kannst den Graph entweder vom Graph der Wurzelfunktion 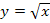ableiten oder du berechnest einige, gut zu berechnende Funktionswerte von 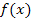, beispielsweise:

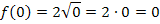
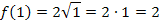
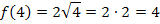
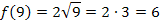
Mit Hilfe dieser Funktionswerte kannst du den Graph leicht in ein Koordinatensystem einzeichnen. Durch die Rotation um die x-Achse entsteht ein Rotationskörper, der einem liegenden Sektkelch (ohne Stiel und Fuß) ähnelt. Deine Skizze sollte ähnlich der folgenden Abbildung sein.

---