3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Zu 3a.)
Im Folgenden dürfen wir für k keine konkrete Zahl mehr einsetzen, denn wir sollen schließlich das Volumen des Rotationskörpers in Abhängigkeit von k berechnen. Das bedeutet, dass wir mit k so rechnen sollen, als wäre es eine feste Zahl;einsetzen dürfen wir aber nichts für k. Wir müssen also mit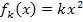 
mit x 
[0;2] und k >0 arbeiten.
Volumenberechnung des Rotationskörpers in Abhängigkeit von k:
Wir berechnen das gesuchte Volumen mit Hilfe der Integralrechnung. Dazu verwenden wir wieder die Formel:
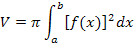
Die Integrationsgrenzen sind durch x [0;2] festgelegt.
Es gilt:a = 0 und b = 2
Mit 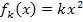ergibt sich für das gesuchte Volumen:
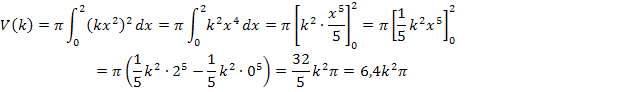
Dir ist der Schritt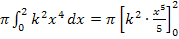 
nicht klar? Ok, dann ganz langsam. Lassen wir mal das 
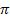vor dem Integral beiseite und betrachten nur das Integral 
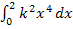. Um das Integral 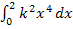zu berechnen, wird die Formel 
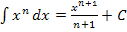verwendet. Das bedeutet nichts anderes, als dass beim Integrieren die Potenz der Variablen x um 1 erhöht und durch den neuen Exponenten geteilt werden soll. (Die additive Konstante „+ C“ können wir weglassen, da es sich bei uns um ein bestimmtes Integral handelt, also um ein Integral mit Grenzen. Dabei braucht man „+ C“ bekanntlich nicht.) Da wir nach dx und nicht etwa nach dk integrieren, darf nur der Exponent von x um 1 erhöht und durch diesen neuen Exponenten dividiert werden. Die Potenz von k bleibt unverändert, denn k ist hier nicht Variable, sondern nur Scharparameter, d.h. k ist als konkrete, feste Zahl zu behandeln! Bei 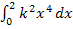ist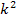 
eine multiplikative Konstante, also quasi eine feste Zahl, mit der multipliziert wird. Multiplikative Konstanten können beim Integrieren einfach abgeschrieben werden. Deshalb wird 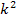bei der Berechnung von 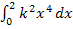abgeschrieben und nur 
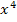wird integriert. Daher gilt: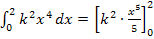 
In einem weiteren Rechenschritt werden dann noch die Grenzen 2 und 0 für x eingesetzt. Zuerst die obere Grenze 2 einsetzen, dann die untere Grenze 0 einsetzen und abziehen.
Der Trichter besitzt somit ein Volumen von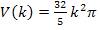 
bzw.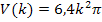 
.
Zu 3b.)
Wir denken uns den Rotationskörper senkrecht aufgerichtet, also um 90° nach oben gedreht. Dann haben wir eine Art Trichter vor uns, den man mit einer Flüssigkeit befüllen kann, ohne dass gleich wieder alles herausläuft.
Der Trichter soll nun bis zur halben Höhe mit Wasser gefüllt werden. Gesucht ist derjenige Bruchteil des gesamten Trichtervolumens, der dann mit Wasser gefüllt ist. Die gesamte Höhe des Trichters ist 2 LE (Längeneinheiten);entsprechend ist die halbe Höhe 1 LE.
