Das bestimmte und das unbestimmte Integral

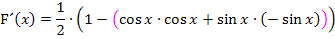
In der anderen Schreibweise ist es etwas übersichtlicher, weil weniger Klammern nötig sind:

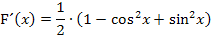
Da wir letztendlich auf 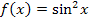kommen wollen, wenden wir einen kleinen Trick an. Wir nehmen den sogenannten „trigonometrischen Pythagoras“ 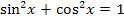zu Hilfe und stellen nach 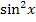um:

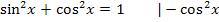
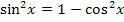
Der Ausdruck 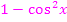kommt auch in 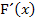vor. Wir ersetzen ihn durch .

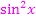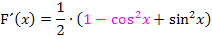
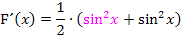
Noch ein klein wenig zusammengefasst und ausgerechnet:

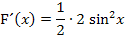
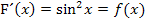
Damit ist bewiesen, dass 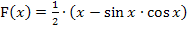eine Stammfunktion der Funktion 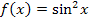ist.

Zugegeben, das war nicht so einfach. Doch darum wurde es ja auch extra auf dieser website gezeigt. (Zur Übung kannst du alleine zeigen, dass 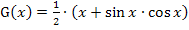eine Stammfunktion der Funktion 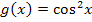ist. Das geht nach dem gleichen Prinzip, hat aber mit unserer Aufgabe nichts zu tun.)

Nun müssen wir noch das Integral 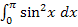berechnen. Wir kennen ja die Stammfunktion zu 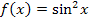. Sie ist 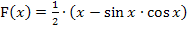, das haben wir schließlich oben bewiesen. Diese Stammfunktion verwenden wir nun bei der Berechnung des Integrals;sie wird in die eckigen Klammern geschrieben. Danach werden in F die Grenzen eingesetzt;zuerst die obere Grenze, dann minus die untere.

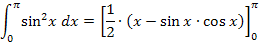
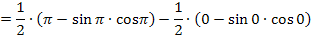
Es gilt:

Damit ergibt sich:

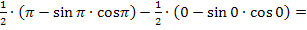
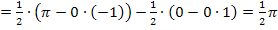
Somit wissen wir: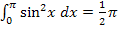

Fertig!

9. Bsp.:Grenzen gesucht bei Integralen trigonometrischer Funktionen

Für welche b ℝ gilt jeweils

a.)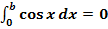

b.)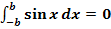

Lösung:

Diese Aufgabe lässt sich entweder durch Rechnung oder durch bloße Überlegung lösen. Nur durch Überlegung geht´s natürlich schneller. Daher wählen wir hier diesen Weg. Ein bestimmtes Integral ergibt Null, wenn die Flächenbilanz gleich Null ist. Die Flächenbilanz ist wiederum gleich Null, wenn entweder obere und untere Grenze gleich sind, oder wenn die Flächen zwischen 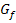und der x-Achse, die oberhalb der x-Achse liegen, genauso großsind wie diejenigen, die unterhalb der x-Achse liegen. Dabei kommt es natürlich darauf an, wo die untere Grenze des Integrals liegt. Die untere Grenze entspricht schließlich dem einen Rand der Fläche zwischen 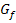und der x-Achse.

Zu 9a.)

Hier noch einmal das gegebene Integral: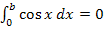

Die Integrandenfunktion ist hier die Kosinusfunktion 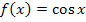. Die Kosinusfunktion ist eine periodische Funktion mit der Periodenlänge 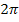, d.h. der Graph von 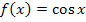ist eine sich ständig wiederholende Schwingung. Eine Schwingung hat genau die Länge 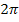, ab dann kommt wieder die gleiche Schwingung. Schauen wir uns den Graph von 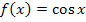doch einfach ´mal an!

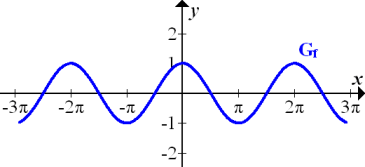
Abb.:Graph der Kosinus-Funktion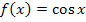

Die Frage ist nun, für welche Werte die Gleichung 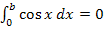erfüllt ist, also für welche Werte von b das Integral Null ergibt.

---