Das bestimmte und das unbestimmte Integral
Das Integral ist gleich Null, wenn entweder die obere mit der unteren Grenze zusammenfällt oder die Flächenbilanz gleich Null ist.
Die beiden Grenzen fallen zusammen, wenn b = 0 gewählt wird. Dann ist die Gleichung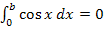 
auf jeden Fall erfüllt. Die erste Lösung der Gleichung lautet somit:b = 0
Nun suchen wir die restlichen Lösungen. Wir überlegen uns, für welche Werte von b die Flächenbilanz gleich Null wird. In anderen Worten:Wir fragen uns, wie weit man auf der x-Achse gehen muss, bis sich die Flächen oberhalb und unterhalb der x-Achse gegenseitig aufheben.
Die untere Grenze des Integrals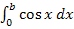 
liegt bei x = 0. Das bedeutet, dass wir in Gedanken bei der y-Achse beginnen. Zuerst beschäftigen wir uns mit den positiven Lösungen von b. D.h. wir gehen von der y-Achse aus auf der x-Achse nach rechts. Dann muss man bis 
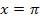gehen, damit das zwischen 
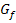und der x-Achse liegende Flächenstück oberhalb der x-Achse (in der nächsten Abbildung grün markiert) genauso großist wie das unterhalb der x-Achse liegende Flächenstück (in der nächsten Abbildung rosa markiert).
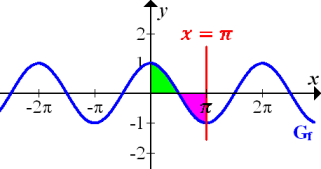
Abb.:Graph der Kosinus-Funktion 
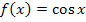
Das grüne Flächenstück ist genauso großwie die rosa Fläche. Das oberhalb der x-Achse liegende grüne Flächenstück geht positiv in die Flächenbilanz ein, das unterhalb der x-Achse liegende rosafarbene Flächenstück negativ. Die beiden Flächenstücke heben sich in der Flächenbilanz gegenseitig auf. Die Flächenbilanz von x = 0 bis 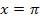ist deshalb gleich Null und somit gilt: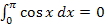 
Die erste positive Lösung der Gleichung 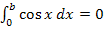lautet somit:b = 
.
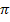Geht man bis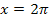 
wird die Flächenbilanz ebenfalls gleich Null.
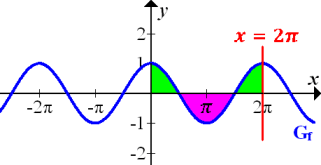
Abb.:Graph 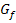der Kosinus-Funktion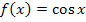
Die beiden grünen Flächenstücke sind zusammen genauso großwie die rosa Fläche. Die Flächenbilanz von x = 0 bis 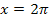ist deshalb gleich Null und somit gilt: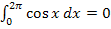 
Setzt man bei 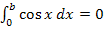für die obere Grenze b den Wert 
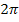ein, ist die Gleichung erfüllt. Die zweite positive Lösung lautet somit: 
.
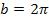Ab 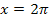wiederholt sich der Graph der Kosinus-Funktion immer wieder. Man sagt, die Funktion ist periodisch mit der Periodenlänge 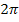. Deswegen muss es zu 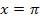und 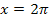jeweils im Abstand von 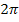weitere Lösungen geben. Die nächsten Lösungen liegt demnach bei 
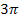und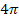 
.
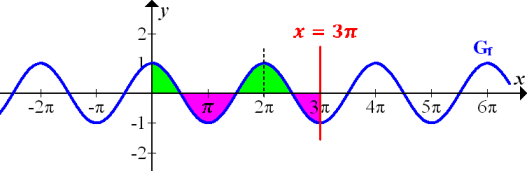
Alle grünen Flächenstücke gemeinsam sind genauso großwie die rosafarbenen Flächenstücke zusammen. Die Flächenbilanz von 0 bis 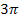ergibt Null, weil die Flächenstücke oberhalb der x-Achse positiv in die Flächenbilanz eingehen und die Flächenstücke unterhalb der x-Achse negativ.
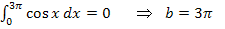
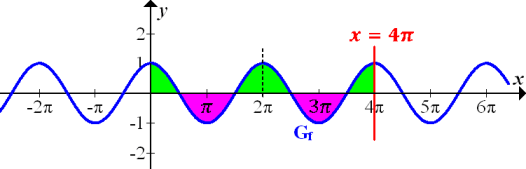
Alle grünen Flächenstücke gemeinsam sind genauso großwie die rosafarbenen Flächenstücke zusammen.
