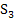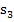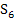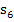Das Summenzeichen und die Streifenmethode

Die Summe der zu kleinen Rechtecksflächen nennen wir Untersumme s. Bei der Untersumme geht man immer vom niedrigsten Kurvenpunkt innerhalb des jeweiligen Streifens aus, um die Höhe des jeweiligen Streifens zu erhalten.

Die Anzahl der Streifen wird mit n bezeichnet;die Streifenbreite nennen wir .

Noch etwas genauer:Die Obersumme bei Verwendung von n Streifen heißt 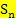;die Untersumme bei n Streifen wird 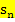genannt. ( So bedeutet beispielsweise 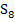„Obersumme mit 8 Streifen“. 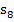steht entsprechend für „Untersumme mit 8 Streifen“.)

Auf dieser website sind diejenigen Flächen, welche den Ober- bzw. Untersummen entsprechen immer grau unterlegt dargestellt. (Die exakten gesuchten Flächen sind dagegen immer grün unterlegt.)

Hier kannst du an einigen Beispielen sehen, wie man eine Obersumme bzw. Untersumme einzeichnet. Die oberen beiden Bilder der folgenden Abbildung zeigen Ober- und Untersumme mit 3 Streifen. Die unteren beiden Bilder zeigen Ober- und Untersumme mit 6 Streifen.

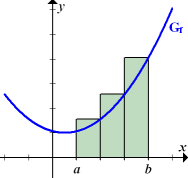
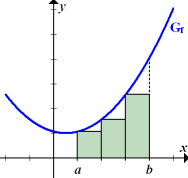
Obersumme	Untersumme
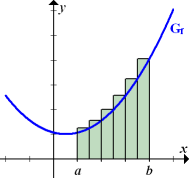
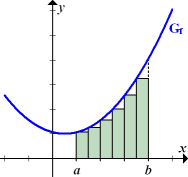
Obersumme	Untersumme

Je höher die Anzahl n der Streifen desto schmäler werden die Rechtecke, d.h. desto kleiner wird die Streifenbreite . Je mehr Streifen wir verwenden, also je kleiner die Streifenbreite , desto genauer nähern wir uns mit dieser Methode an den Inhalt der tatsächlichen Fläche A an. Mit steigender Anzahl n der Streifen wird die Obersumme 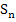immer kleiner und die Untersumme 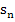immer größer. Lässt man die Anzahl n der Streifen gegen Unendlich gehen, nähern sich sowohl die Obersumme 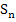als auch die Untersumme 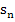dem exakten Flächeninhalt A an. Die Grenzwerte 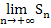und 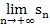liefern das exakte Ergebnis des Integrals .

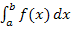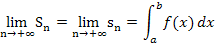
Mit Hilfe der Streifenmethode können somit Formeln hergeleitet werden, mit deren Hilfe wir bestimmte Integrale berechnen können. Das Ergebnis des Integrals entspricht dabei anschaulich dem Inhalt der Fläche A zwischen und der x-Achse von der senkrechten Geraden x = a bis zur senkrechten Geraden x = b. (Immer noch vorausgesetzt, dass die Fläche vollständig oberhalb der x-Achse liegt.)

Zur Vereinfachung wählen wir vorerst a = 0. Anschaulich bedeutet das, dass wir bei der y-Achse beginnen. (Die y-Achse hat schließlich die Gleichung x = 0.)

Beispiel für die Berechnung eines Integrals mit der Streifenmethode:

Betrachten wir nun als konkretes Beispiel die Funktion 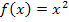. Ihr Graph ist eine nach oben geöffnete Normalparabel, ihr Scheitel S liegt im Ursprung.

---