Das Summenzeichen und die Streifenmethode
Für i = 1 ergibt der Term 2i – 1 die Zahl 1 und für i = 6 die Zahl 11. i muss bei dem Term 2i – 1 demnach alle natürlichen Zahlen von 1 bis 6 durchlaufen, um die ungeraden Zahlen von 1 bis 11 zu ergeben.
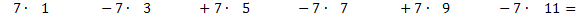
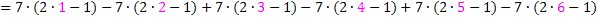
Wären alle Vorzeichen positiv, könnte man die Summe von i = 1 bis i = 8 von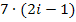 
bilden.
Was ist nun aber mit den Vorzeichen? Bei Gliedern mit ungeradem i steht jeweils ein Plus, bei Gliedern mit geradem i steht ein Minus. Die entsprechenden Vorzeichen ergeben sich durch Multiplikation mit dem Ausdruck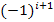 
oder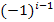 
. Wir entscheiden uns hier für die Verwendung von .
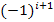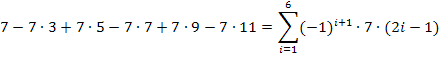
Natürlich gibt es noch weitere Lösungen dieser Teilaufgabe, doch wollen wir uns mit den beiden soeben gezeigten Möglichkeiten begnügen. Du konntest auf jeden Fall sehen, dass es oft verschiedene Möglichkeiten gibt, einen gegebenen Term mit einem Summenzeichen zu schreiben. Du bist nun hoffentlich soweit mit dem Summenzeichen und dem Umgang mit endlichen Reihen vertraut, dass wir einen Schritt weitergehen können.
Als nächstes gilt es eine Möglichkeit zu finden, wie man das Ergebnis bestimmter Reihen mit sehr vielen Gliedern schneller ausrechnen kann als durch normales nacheinander Addieren der einzelnen Glieder. Wie bereits oben angesprochen, gibt es da einen wesentlich schnelleren Weg (insbesondere bei Summen von Potenzen, wie zum Beispiel der Summe von n natürlichen Zahlen oder ihrer zweiten, dritten bzw. vierten Potenz).
Gehen wir noch einmal zurück zu unserem zweiten Einführungsbeispiel. Es ging darum, die Summe der ersten hundert natürlichen Zahlen zu berechnen.
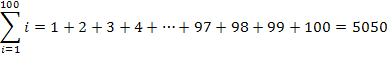
Wie kommt man nun auf das Ergebnis 5050, wenn man nicht der Reihe nach alle natürlichen Zahlen von 1 bis 100 addieren will, weil einem das zu viel Arbeit ist?
Bereits vor langer Zeit hatte da ein Schüler, der von seinem Lehrer diese Aufgabe gestellt bekam, eine zündende Idee. (Dieser Schüler wurde später allerdings zu einem berühmten Mathematiker.) Hast du auch eine? Überleg erst mal selbst!
Keine Idee? Dann hier die Lösung des Problems:
Man addiert jeweils die Zahl 1 zu der Zahl 100, die Zahl 2 zu der Zahl 99, die Zahl 3 zur Zahl 98, die Zahl 4 zur Zahl 97 usw. Das ergibt jeweils 101. Da wir jeweils zwei der hundert Zahlen zu einem Pärchen mit der Summe 101 zusammengefasst haben, liegen nun 50 Pärchen vor, die alle jeweils die Summe 101 haben. Wir müssen also nur noch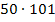 
rechnen und schon sind wir fertig.
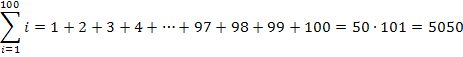
Um allgemein eine Formel für die Summe der natürlichen Zahlen von 1 bis n zu entwickeln, schauen wir uns das Ganze noch etwas genauer an.
