Die Integralfunktion und der HDI
Von der unteren Grenze ausgehend, überlegt man sich, bis wie weit man auf der x-Achse gehen müsste, damit die Fläche oberhalb genauso großwird wie die unter der x-Achse. Dann heben sich die Flächen praktisch gegenseitig auf;die Flächenbilanz und somit das Integral ist dann gleich Null. Es liegt eine Nullstelle von F vor. (Falls die Fläche zwischen 
und der x-Achse vollständig oberhalb oder vollständig unterhalb der x-Achse liegt, hat die Integralfunktion F keine weiteren Nullstellen. Dann gibt es keine Flächen, die sich gegenseitig aufheben. Die untere Grenze ist dann die einzige Nullstelle von F. Das ist immer dann der Fall, wenn der Graph der Integrandenfunktion f die x-Achse nicht schneidet. Das gleiche gilt auch, wenn die Integrandenfunktion f die x-Achse zwar genau einmal schneidet, diese Nullstelle jedoch mit der unteren Grenze von F zusammenfällt.)
Als erstes musst du also schauen, wo die untere Grenze von F liegt. Das ist sehr wichtig! In diesem Fall ist die untere Grenze bei x = – 2. (Durch die Gleichung x = – 2 ist eine senkrechte Gerade beschrieben, welche die x-Achse bei – 2 schneidet.) Von x = – 2 ausgehend, überlegst du dir jetzt, wie weit du nach links oder rechts auf der x-Achse gehen musst, damit die Flächenstücke oberhalb und unterhalb der x-Achse gleich großwerden, sich also in der Flächenbilanz gegenseitig aufheben.
Hier noch einmal der Graph der Funktion f . Miteingezeichnet ist auch die untere Grenze von F, d.h. die Gerade x = – 2.
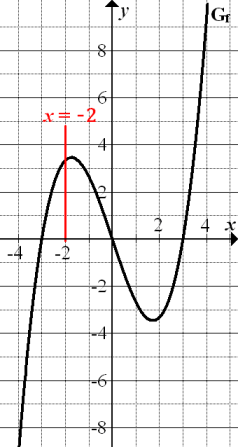
Abb.:Graph der Funktion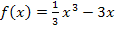 
und die senkrechte Gerade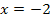 
Der Graph der Funktion 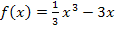ist punktsymmetrisch zum Ursprung. Das ist an der Abbildung sofort zu erkennen, aber auch an der Funktionsgleichung von f , denn es treten nur ungerade Potenzen von x auf. Aus der Punktsymmetrie des Graphen folgt, dass die Fläche zwischen und der x-Achse von x = – 2 bis x = 0 genauso großist wie die Fläche zwischen und der x-Achse von x = 0 bis x = 2. Die eine Fläche (lila markiert in der folgenden Abbildung) liegt oberhalb, die andere (rosa markiert in der folgenden Abbildung) unterhalb der x-Achse. Somit muss die Flächenbilanz gleich Null werden, wenn man bis x = 2 geht. Daher gilt: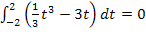 
Bei x = 2 liegt zwangsläufig eine weitere Nullstelle von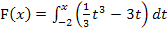 
.
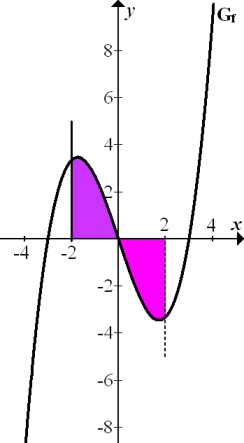
Abb.:Graph der Funktion 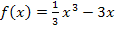und die Geraden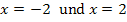 
Nun ist die Frage, ob es noch mehr Nullstellen von F gibt, und wenn das der Fall ist, wo diese ungefähr liegen. Es ist also zu überlegen, wie weit man auf der x-Achse gehen muss, dass sich (wenn man bei x = – 2 beginnt) die Flächenstücke zwischen und der x-Achse, die oberhalb der x-Achse liegen, mit denen unterhalb der x-Achse praktisch gegenseitig aufheben.
