Uneigentliche Integrale

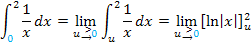
Als nächstes werden die Grenzen eingesetzt;die Obere minus die Untere. Da die Zahl 2 sowieso schon positiv ist, ist der Betrag von 2 natürlich 2;die Betragsstriche sind bei 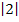unnötig. Auch bei 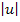können die Betragsstriche weggelassen werden, aber nur weil u hier für eine positive Zahl steht. u ist hier positiv wegen der rechtsseitigen Annäherung an die Null.

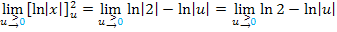
Als letztes wird der Grenzwert ermittelt. Stelle dir dazu den Graph der Funktion 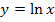vor und überlege dir, was 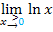ist, also wie sich der Graph von rechts kommend in der Nähe von x = 0, d.h. ein klein wenig rechts von der y-Achse, verhält. Ausführliche Erklärungen im Kapitel:Die e-Funktion und ihre Umkehrfunktion die ln-Funktion

Die ln-Funktion schießt für x gegen 0 nach unten, also geht sie gegen 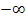. Es gilt daher:

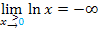
Für unsere Aufgabe folgt damit: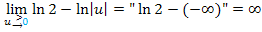

Wir haben so das folgende Ergebnis erhalten: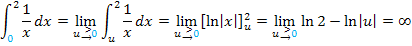

Die Fläche zwischen dem Graphen von 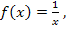der x-Achse, der y-Achse und der senkrechten Gerade x = 2 ist unendlich groß.

Zu 1d.)

Hier tritt ein neues Problem auf:Die Definitionslücke ist nicht eine der Grenzen des Integrals, sondern liegt im Inneren des Integrationsbereichs. Solche Integrale müssen an der Definitionslücke geteilt werden.

Um das Integral 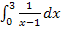zu berechnen, müssen wir es an der Definitionslücke x = 1 aufteilen.

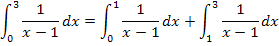
Nun schreiben wir statt der Grenze 1 den Buchstaben u und berechnen den jeweiligen Grenzwert. Beim Integral von 0 bis 1 nähert man sich von links an die Definitionslücke 1 an;daher brauchen wir dabei den linksseitigen Grenzwert 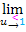. Beim Integral von 1 bis 3 nähert man sich von rechts an die Definitionslücke 1 an;entsprechend bilden wir den rechtsseitigen Grenzwert .

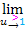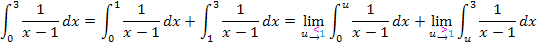
Als nächstes suchen wir nach einer Stammfunktion zu 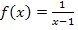. Erfreulicherweise ist der Zähler des Bruchs exakt die Ableitung des Nenners. Es kann die folgende Formel angewendet werden: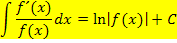

(Ausführliche Erklärung dieser Formel im Teil Weitere Integrationsregeln.)

Damit erhalten wir:

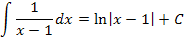
In unserer Aufgabe ergibt sich damit:

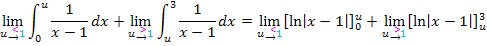
Wir setzen jeweils die Grenzen ein:Obere minus Untere

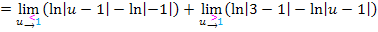
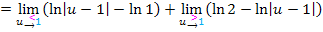
Wegen 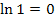vereinfacht sich das Ganze zu:

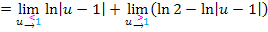
Nun versuchen wir die Grenzwerte zu berechnen.

Zur Erinnerung: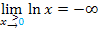

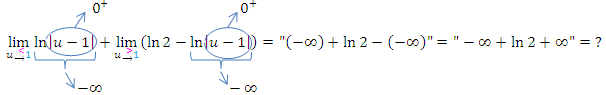
Jetzt stehen wir vor einem Problem:Was ergibt 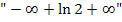? In diesem Fall heben sich 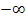und 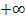tatsächlich auf und es kommt letztendlich ln2 heraus.

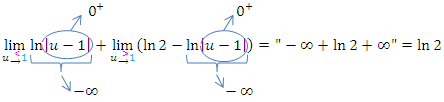
Dass sich hierbei wirklich ln2 ergibt, muss man jedoch erst rechnerisch nachweisen. Man kann nämlich nicht generell sagen, dass 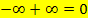gilt. Es hängt davon ab, ob ein Unendlich überwiegt, oder ob sie beide gleich stark sind. Um das besser beurteilen zu können, fassen wir die beiden Grenzwerte zu einem einzigen Limes zusammen. Das darf aber erst gemacht werden, wenn bei beiden Grenzwerten 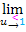oder bei beiden 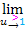steht.

---