1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Wenn man nun das Integral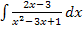 
oder 
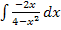ermitteln will, muss sich umgekehrt wieder diejenige Funktion ergeben, die wir ursprünglich abgeleitet haben. Man muss nur einen zusätzlichen Betrag verwenden, damit das Integral für alle reellen Zahlen aus der Definitionsmenge von 
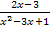bzw. von 
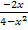gilt. Außerdem darf das „+ C “ nicht vergessen werden.
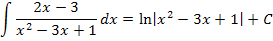
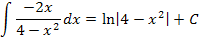
Allgemein lässt sich feststellen:
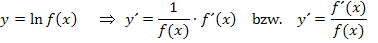
Wenn man das Integral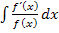 
lösen will, muss sich demnach ergeben:
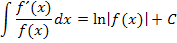
Die Regel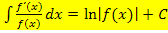 
kannst du immer dann anwenden, wenn du einen Bruch integrieren willst, dessen Zähler die Ableitung des Nenners ist. Im Bruch muss also oben die Ableitung des unteren Terms stehen. Dann ist die Stammfunktion der ln vom Betrag des unteren Terms. Warum ist der Betrag nötig? Die ln-Funktion ist nur für positive Argumente definiert. Einfacher gesagt:Der Ausdruck, auf den sich der ln bezieht, muss größer Null sein. Daher ist der Betrag in der oben gezeigten Formel notwendig. Ist 
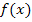allerdings sowieso positiv, kann der Betrag durch eine Klammer ersetzt werden. (Mehr über die ln-Funktion im Kapitel Die e-Funktion und ihre Umkehrfunktion die ln-Funktion) Schauen wir uns doch gleich einige konkrete Beispiele für diese Integrationsregel an.
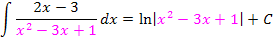
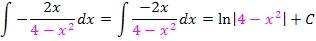
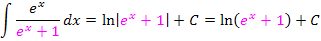
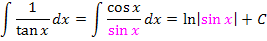
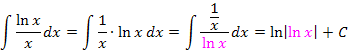
Hinweis zum letzten Beispiel:Die Ableitung von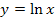 
ist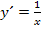 
.
In allen gezeigten Beispielen war letztendlich der Zähler des Bruchs genau die Ableitung des Nenners, daher konnte die Integrationsregel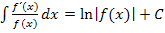 
direkt angewendet werden. (Beim letzten Beispiel war das zu Beginn allerdings schwer zu erkennen. Deshalb wurde dieses Beispiel hier extra vorgeführt. Du solltest es dir gut merken.) Mit einem kleinen Trick lässt sich diese Integrationsregel aber auch dann anwenden, wenn der Zähler nicht genau die Ableitung des Nenners ist, sondern nur ein Vielfaches der Nennerableitung. Man muss dann so erweitern, dass im Zähler doch die Ableitung des Nenners zu stehen kommt. In anderen Worten:Man überlegt sich, was die Ableitung des Nenners ist und schreibt dies in den Zähler;zum Ausgleich setzt man eine Konstante vor das Integral. Wie das genau funktioniert, kannst du an den nächsten Beispielen sehen:
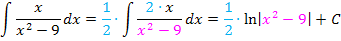
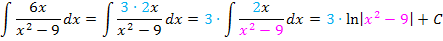
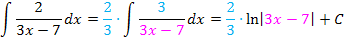
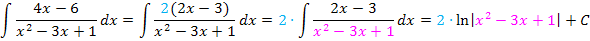
Eigentlich ist das Prinzip gar nicht so schwer. Man muss aber den korrekten Vorfaktor finden, mit dem man multiplizieren muss.
An dieser Stelle passieren erfahrungsgemäßhäufig Fehler! Es wird oft fälschlich mit dem Kehrwert der richtigen Zahl multipliziert. An Stelle von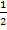 
wird von vielen Schülern beispielsweise mit 2 multipliziert oder mit 3 statt mit 
.
