1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Das letzte Beispiel sollte dir zeigen, dass sich mit Hilfe der Logarithmusrechengesetze Ergebnisse, die einen ln enthalten, oft noch deutlich vereinfachen lassen. Auf diese Umformungen gibt es in Prüfungen Punkte. Also bitte keinesfalls schon vorher aufhören und einfach den Taschenrechner nehmen. Mit dem Taschenrechner kannst du meist sowieso nur einen gerundeten Wert berechnen, jedoch nicht das exakte Ergebnis. Das Eintippen in den Taschenrechner bringt dir nur dann etwas, wenn in der Aufgabenstellung definitiv nach einem gerundeten Wert gefragt ist, also wenn es beispielsweise heißt, runde auf drei Nachkommastellen.
Bisher hatten wir es immer mit Integralen von Brüchen zu tun, deren Zähler entweder genau der Ableitung des Nenners entsprachen oder zumindest ein Vielfaches davon waren. Damit der Zähler einer gebrochenrationalen Funktion genau der Ableitung des Nenners oder einem Vielfachen davon entsprechen kann, muss der Zählergrad um 1 kleiner sein als der Nennergrad. (Der Grad eines Polynoms ist die höchste Potenz der Variablen x.) Beim Ableiten wird schließlich die Potenz von x immer um 1 kleiner. Was ist nun aber mit Brüchen, deren Zählergrad gleich oder sogar größer ist als der Nennergrad? Bei solchen Brüchen steht im Zähler definitiv nicht die Ableitung des Nenners und auch kein Vielfaches davon;die Potenzen von x sind schließlich viel zu hoch.
Nach geeigneter Umformung mittels Ausdividieren z. B. mit einer Polynomdivision oder geschickter Zählerergänzung lassen sich aber auch manche gebrochenrationalen Funktionen integrieren, deren Zähler nicht die Ableitung des Nenners oder ein Vielfaches davon bildet.
Betrachten wir beispielsweise die Funktionen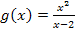 
und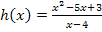 
. Wie kann man sie integrieren? Bei beiden Funktionen ist der Zähler keinesfalls die Ableitung des Nenners. In der Form, in der die Funktionen momentan gegeben sind, kann man sie (noch) nicht mit Hilfe der Regel 
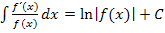integrieren. Es gibt allerdings zwei mathematische Tricks, die uns hier weiterhelfen:
1. Geeignete Zählerergänzung
D.h. man addiert im Zähler eine bestimmte Zahl und subtrahiert sie gleich wieder bzw. umgekehrt, damit sich im Prinzip nichts an der Funktion ändert. Dann spaltet man den Bruch in zwei Teilbrüche auf. Beim ersten kürzt man den Nenner komplett weg;das Ergebnis ist kein Bruch mehr und lässt sich somit leicht integrieren. Beim zweiten entstehenden Teilbruch lässt sich dann die Regel 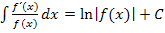anwenden.
