2a. Partielle Integration
8. Bsp.:Berechne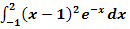 
!
Lösung:
Bevor wir mit der eigentlichen Rechnung beginnen, quadrieren wir die Klammer. Dazu verwenden wir die zweite binomische Formel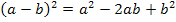 
.
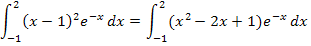
Du siehst, dass der erste Faktor des zu integrierenden Produkts ein Polynom zweiten Grades ist;die höchste Potenz von x ist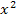 
. Wir werden daher nacheinander zwei partielle Integrationen durchführen müssen, um das Integral zu lösen.
Wichtig ist dabei, dass immer das jeweils vorliegende Polynom mit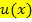 
bezeichnet wird.
Du darfst auf keinen Fall das Polynom bei der ersten partiellen Integration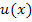 
und dann bei der zweiten partiellen Integration 
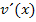nennen! Dann würdest du dich bloßim Kreis drehen, auf die Lösung kämst du so aber nicht.
1. Partielle Integration
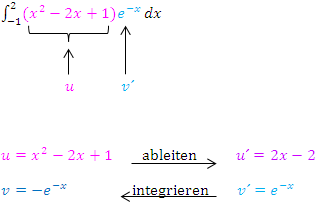
Beachte das Minus-Zeichen bei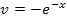 
! Du kommst auf v, indem du 
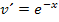integrierst, d.h. indem du das Integral 
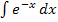berechnest. Es handelt sich um das Integral der lineartransformierte Funktion 
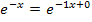. (Ausführlichere Erklärungen weiter oben im Bsp. 5h und 5i.)
Wir setzen ein in die Formel: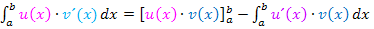 
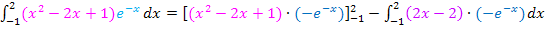
Das Minus von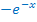 
ziehen wir jeweils nach vorne.
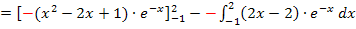
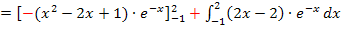
Den vorderen Teil kann man direkt ausrechnen;man muss nur noch die Grenzen einsetzen. Den hinteren Teil, also das neue Integral muss man mit einer zweiten partiellen Integration lösen.
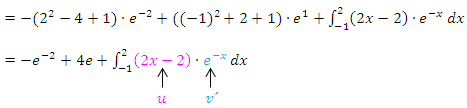
2. Partielle Integration
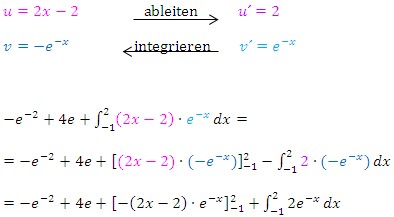
In den mittleren Ausdruck müssen nur noch die Grenzen eingesetzt werden. Das noch vorliegende Integral lässt sich nun endlich auf herkömmlichen Weg ausrechnen. Zu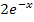 
ist schließlich 
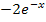eine Stammfunktion. Eine weitere partielle Integration ist nicht nötig.
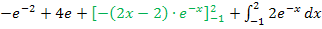
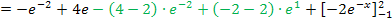
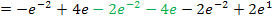
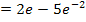
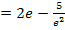
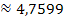
9. Bsp.:Ermittle die Menge aller Stammfunktionen F der Funktion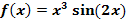 
!
Lösung:
Wir müssen das folgende unbestimmte Integral lösen: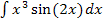 
Die Funktion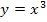 
ist ein Polynom dritten Grades. Die Funktion 
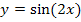ist eine Funktion, die sich leicht integrieren lässt, da es sich um eine lineartransformierte Funktion handelt. (Siehe „Integration einiger Sonderfälle“ 5. Bsp. weiter oben!) Das Integral 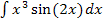hat also die folgende Form: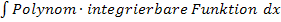 
Das Polynom nennen wir wieder u und den anderen Faktor v´. Da es sich um ein Polynom dritten Grades handelt, sind insgesamt drei partielle Integrationen nötig.
Das neu entstandene Integral wird wieder mit einer weiteren partiellen Integration berechnet.
Das neu entstandene Integral wird mit einer letzten partiellen Integration gelöst.
Vorsicht:Vor dem Integral steht ein Minus!
