Einfachere Variante der Integration durch Substitution
Diese Methode eignet sich für Integrale der Form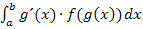 
. Die Funktion 
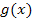ist die innere Funktion und ihre Ableitung 
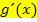steht bereits da. Genauer gesagt, muss 
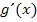ein Faktor der zu integrierenden, verketteten Funktion sein. Auch wenn ein Vielfaches der Ableitung 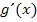da steht, klappt dieses Verfahren. Am besten schauen wir uns gleich ein konkretes Beispiel an.
15. Bsp.:Berechne das folgende bestimmte Integral mit Hilfe einer geeigneten Substitution!
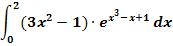
Lösung:
Die innere Funktion 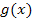ist hier die Funktion, die im Exponenten der e-Funktion steht, also 
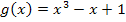. Ihre Ableitung 
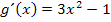steht auch schon da. Deshalb substituieren wir folgendermaßen:
1. Schritt:Substitution
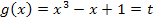
Den Ausdruck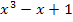 
nennen wir also 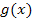bzw. t.
2. Schritt: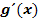 
bilden und mit dx erweitern
Wir schreiben nun die Ableitung von 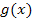hin und erweitern in einem nächsten Schritt mit dem Ausdruck dx. Das bedeutet, dass wir auf beiden Seiten dx dazu schreiben. (Warum wir das machen, wird gleich noch klar.)
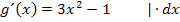
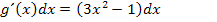
3. Schritt:Gleich dt setzen und nach dx auflösen
Die rechte Seite der obigen Gleichung setzen wir jetzt gleich dt und lösen dann nach dx auf.
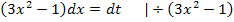
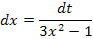
Den Ausdruck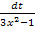 
werden wir später, wenn wir das Integral letztendlich lösen, für dx einsetzen. Da die Ableitung von 
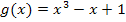, also 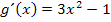, auch bei der zu integrierenden Funktion vorkommt, lässt sich 
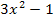dann wegkürzen. Das ist entscheidend, denn wir wollen letztendlich ein Integral erzeugen, das ausschließlich t als Variable enthält, aber kein x mehr.
4. Schritt:Neue Grenzen berechnen durch Einsetzen der alten Grenzen in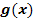 
Es liegt hier ein bestimmtes Integral vor;wir haben schließlich die untere Grenze 0 und die obere Grenze 2 gegeben. Diese Grenzen beziehen sich allerdings auf die Variable x. Wir passen sie nun an die neue Variable t an, indem wir sie in 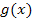einsetzen. Das Ergebnis der unteren Grenze wird zur neuen unteren Grenze, das Ergebnis der oberen Grenze entsprechend zur neuen oberen Grenze. (Es kann sein, dass die neue obere Grenze kleiner wird als die neue untere, obwohl ursprünglich die obere Grenze größer war als untere. Dann darfst du trotzdem die Grenzen nicht vertauschen!
