Einfachere Variante der Integration durch Substitution
16. Bsp.:Berechne mittels Integration durch Substitution!
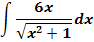
Lösung:
Bei einem unbestimmten Integral gibt es keine Grenzen. Daher entfällt der 4. Schritt, also die Berechnung der neuen Grenzen. An statt der Berechnung der neuen Grenzen muss bei unbestimmten Integralen allerdings eine Rücksubstitution vorgenommen werden. D.h. man muss am Ende jedes auftretende t wieder durch das jeweilige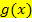 
ersetzen.
1. Schritt:Geeignete Substitution durchführen
Der Ausdruck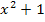 
, der unter der Wurzel steht, ergibt abgeleitet 
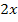. Im Zähler der zu integrierenden Funktion steht 
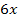;das ist zwar nicht genau die Ableitung des Ausdruck unter der Wurzel, aber ein Vielfaches davon, genau genommen das Dreifache. Daher setzen wir 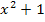gleich 
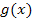bzw. t.
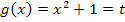
2. Schritt:Bilde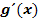 
und erweitere mit dem Ausdruck dx.
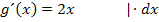
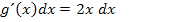
3. Schritt:Setze den erhaltenen Ausdruck gleich dt und löse nach dx auf.
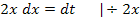
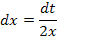
4. Schritt:Berechnung der neuen Grenzen entfällt;stattdessen wird nachher eine Rücksubstitution durchgeführt
5. Schritt:Berechnung des Integrals
Der Ausdruck 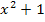wird durch t ersetzt. Statt dx schreiben wir 
.
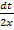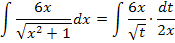
Nun lässt sich 2x kürzen. Es ergibt sich ein Integral, das nur noch die neue Variable t enthält.
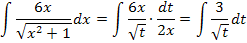
Wir formen mit den Potenzgesetzen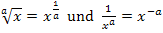 
um, damit wir dann das Integral mit der Formel 
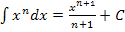lösen können.
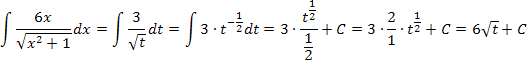
Nun erfolgt die Rücksubstitution;wir ersetzen t wieder durch 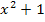. Wir müssen schließlich zurück zur ursprünglichen Variablen x kommen, da es sich um ein unbestimmtes Integral handelt.
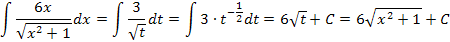
Hinweis:Das soeben gezeigte Verfahren mit der Rücksubstitution kann auch bei bestimmten Integralen angewendet werden. Dann dürfen die Grenzen allerdings nicht verändert werden. Bei bestimmten Integralen kann man daher zwischen zwei Rechenwegen wählen:Ohne Rücksubstitution, aber mit veränderten Grenzen oder mit Rücksubstitution und den ursprünglichen Grenzen. Das ist reine Geschmackssache.
Nun wollen wir uns noch ein anspruchsvolleres Beispiel ansehen. Es ist allerdings nur für Schüler geeignet, welche im Unterricht bereits die Umkehrfunktionen der trigonometrischen Funktionen behandelt haben. Du solltest also die folgenden Funktionen kennen:
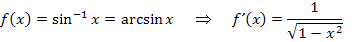
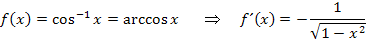
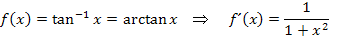
Daher gelten folgende Grundintegrale:
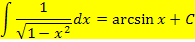
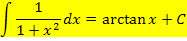
Diese Integrale ermöglichen es uns auch bestimmte, schwierigere Aufgaben durch geeignete Substitution zu lösen. Schauen wir uns ein paar konkrete Beispiele dafür an.
17. Bsp.:Berechne eine Stammfunktion von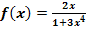 
!
