Schwierigere Variante der Substitution
) dauern, bis man die Lösung findet. Auch erfahrene Mathematiker brauchen bei extrem schwierigen Integralen sehr lange, bis sie die Lösung gefunden haben. Das hängt eben vom Integral ab. Doch so schwere Aufgaben werden dir in Prüfungen sicher nicht gestellt. Wir werden im Folgenden eine machbare Aufgabe besprechen und daran das Prinzip vorführen. Also keine Sorge, wenn du bisher das Prinzip der Substitution (Variante 2) noch nicht wirklich verstanden hast. Wir machen das jetzt gleich noch einmal alles Schritt für Schritt an einem konkreten Beispiel.
19. Bsp.:Berechne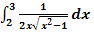 
! Verwende dabei die Substitution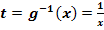 
Lösung:
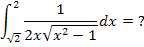
Wenn du dich nun wunderst, warum wir nicht die einfache 1. Variante der Substitution anwenden, weil du dir denkst, dass die Ableitung von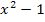 
, also 
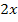doch schon da steht, musst du nur etwas genauer hinsehen. 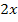steht im Nenner! Du musst das als 
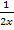auffassen und das ist nicht die Ableitung von .
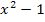Wenn du die 1. Variante der Substitution versuchst und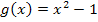 
wählst, wird sich am Schluss 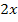nicht wegkürzen. Es würde ein Integral mit x und t entstehen. Das lässt sich natürlich nicht lösen. Diese Variante würde also nicht klappen!
Das ist dir nicht klar? Ok, dann machen wir das gemeinsam, obwohl es natürlich nicht zur Lösung führt.
Substitution (Variante 1)
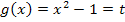
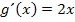
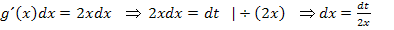
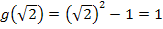
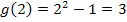
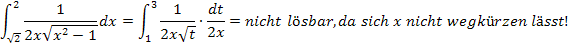
Wir müssen daher die schwierigere Variante der Substitution anwenden. Erfreulicherweise ist eine passende Substitution schon in der Aufgabenstellung angegeben. Du musst also hier nicht selbst auf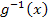 
kommen.
1. Schritt:Geeignete Substitution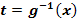 
durchführen und nach x auflösen;das ergibt 
.
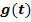Laut Angabe ist die folgende Substitution zu wählen:
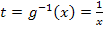
Auflösen nach x ergibt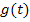 
.
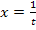
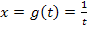
2. Schritt: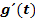 
bilden
Mit dem Potenzgesetz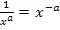 
formen wir 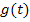um, so dass wir die Ableitungsregel 
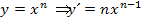verwenden können.
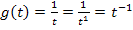
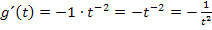
3. Schritt:dx gleich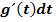 
setzen
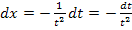
4. Schritt:Ursprünglichen Grenzen a und b in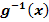 
einsetzen. Das ergibt die neuen Grenzen 
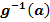und 
.
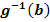Die Grenzen des zu berechnenden Integrals sind ursprünglich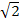 
(untere Grenze) und 2 (obere Grenze). Die ursprünglichen Grenzen beziehen sich auf die Variable x. Wir müssen sie an die neue Variable t anpassen. Dazu setzen wir sie jeweils für x in 
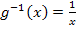ein. So bekommen wir die neuen Grenzen.
Neue untere Grenze: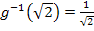 
Neue obere Grenze: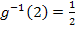 
5. Schritt:Ersetze im Integranden (d.h. in der zu integrierenden Funktion) jedes x durch 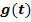und versuche das Integral mit den neuen Grenzen 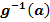und 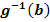zu lösen.
Jetzt wird es spannend, denn erst nach diesem Schritt merkt man, ob die Substitution etwas gebracht hat oder nicht.
