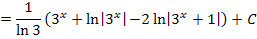Schwierigere Variante der Substitution
(Multiplikative Konstanten bleiben beim Ableiten bekanntlich immer stehen.)
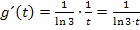
Mit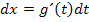 
ergibt sich: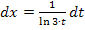 
Nun versuchen wir die Integration.
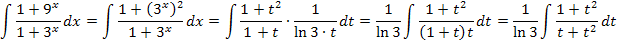
Dieses Integral ist lösbar. Um es lösen zu können, müssen wir den Integranden aber erst noch umformen. Zuerst führen wir eine Polynomdivision durch, da es sich um eine unechtgebrochenrationale Funktion (Zählergrad größer oder gleich Nennergrad) handelt. (Siehe auch:Gebrochenrationale Funktion)
Bevor wir den Bruch mittels Polynomdivision ausrechnen können, müssen jedoch sowohl im Zähler als auch im Nenner die Potenzen absteigend geordnet werden;sonst klappt die Polynomdivision nicht.
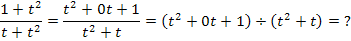
Nebenrechnung (Polynomdivision):
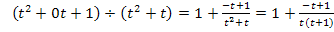
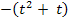
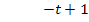
Die Polynomdivision ist nicht aufgegangen;aber das macht nichts. Den Restbruch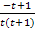 
müssen wir allerdings mit Hilfe einer Partialbruchzerlegung noch weiter umformen, bevor wir integrieren können. Damit ist gemeint, dass wir den Bruch 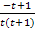als Summe zweier Einzelbrüche, also in der Form 
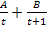schreiben wollen. Dann lässt sich nämlich besser integrieren. Dazu müssen wir natürlich herausfinden, was A und B hier ist. Du weißt bestimmt, wie man 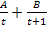auf einen gemeinsamen Bruch bringen kann. Man muss einfach entsprechend erweitern. Die Partialbruchzerlegung von 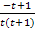ist praktisch das Gegenteil davon. Man will wieder rückwärts auf die Einzelbrüche kommen. Wie das funktioniert, wird nun vorgeführt.
Nebenrechnung (Partialbruchzerlegung):
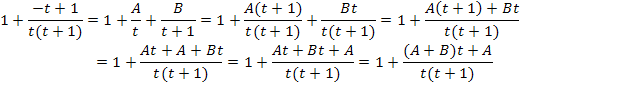
Nun führen wir einen Koeffizientenvergleich durch, um A und B zu ermitteln. Das bedeutet, dass du die Zahlen bzw. Ausdrücke vergleichen sollst, die jeweils im Zähler des ursprünglichen Bruchs 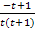und beim Zwischenergebnis 
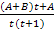vor der Variablen t stehen und diejenige Zahl bzw. denjenigen Buchstaben, der ohne t vorkommt.
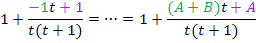
Durch den Koeffizientenvergleich erhalten wir zwei Gleichungen, für die beiden Unbekannten A und B.
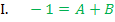
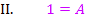
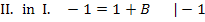
Die berechneten Werte A = 1 und B = -2 setzen wir in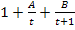 
ein. So ergibt sich:
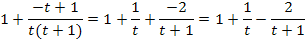
Wir haben den Integranden durch Polynomdivision und anschließender Partialbruchzerlegung also folgendermaßen umgeformt:
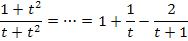
Nun können wir leicht integrieren, da sich beide verbliebenen Brüche gut integrieren lassen.
ergibt integriert bekanntlich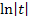 
. Beim zweiten Bruch ist der Zähler das Doppelte, also ein Vielfaches der Ableitung des Nenners;wir integrieren den zweiten Bruch daher mit der Formel 
.
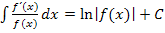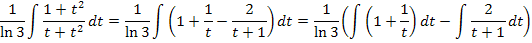
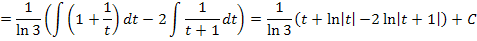
Als letztes führen wir die Rücksubstitution durch:Wir schreiben statt t wieder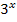 
.
