Schwierigere Variante der Substitution
Wir greifen ´mal wieder tief in die mathematische Trickkiste und verwenden folgende zwei Formeln:
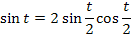
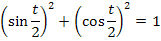
Statt 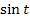 im Nenner des Integranden schreiben wir
im Nenner des Integranden schreiben wir 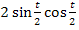 . Statt der Zahl 1 im Zähler des Integranden schreiben wir
. Statt der Zahl 1 im Zähler des Integranden schreiben wir 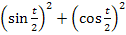 .
.
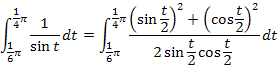
Nun denkst du dir vermutlich, dass das nun vorliegende Integral ja noch viel komplizierter ist als das schöne kleine Integral von vorher. Aber in Wirklichkeit lässt sich das neue Integral mit der Formel 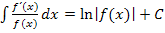 gut lösen. Die Frage ist nur, wie diese Formel hierbei weiter hilft. Leite doch schnell den Nenner des Integranden ab und vergleiche mit dem Zähler!
gut lösen. Die Frage ist nur, wie diese Formel hierbei weiter hilft. Leite doch schnell den Nenner des Integranden ab und vergleiche mit dem Zähler!
Passt das bereits? Leider nein, denn ein Vorzeichen stimmt nicht. Die Ableitung des Nenners ist nämlich 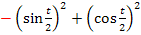 und nicht
und nicht 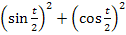 . Die Ableitung des Nenners ist auch kein Vielfaches des Zählers. Damit es das Minus-Eins-fache wäre, müsste nämlich sowohl vor dem Sinus als auch vor dem Kosinus ein Minuszeichen stehen.
. Die Ableitung des Nenners ist auch kein Vielfaches des Zählers. Damit es das Minus-Eins-fache wäre, müsste nämlich sowohl vor dem Sinus als auch vor dem Kosinus ein Minuszeichen stehen.
Du hast Probleme beim Ableiten von 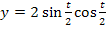 ?
?
Ok, dann machen wir das gemeinsam! Wir brauchen einerseits die Produktregel, da die Variable t in beiden Faktoren des Produkts auftritt, und andererseits die Kettenregel, da sowohl der erste Faktor 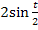 als auch der zweite Faktor
als auch der zweite Faktor 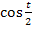 eine verkettete Funktion ist. Die jeweils innere Funktion, also
eine verkettete Funktion ist. Die jeweils innere Funktion, also 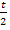 , muss daher nachdifferenziert werden.
, muss daher nachdifferenziert werden.
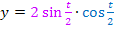
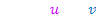
Produktregel: 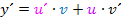
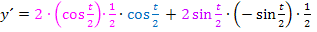
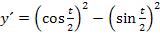
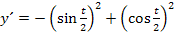
Wir müssen uns daher etwas anderes einfallen lassen, um das Integral 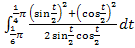 zu lösen. Wir teilen den Integranden in zwei einzelne Brüche auf, kürzen dann jeweils so weit möglich und schon schaut die Sache besser aus.
zu lösen. Wir teilen den Integranden in zwei einzelne Brüche auf, kürzen dann jeweils so weit möglich und schon schaut die Sache besser aus.
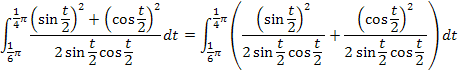
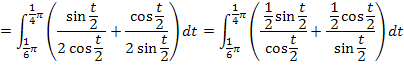
Der Nenner des ersten Integrals ist 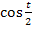 ;mit der Kettenregel abgeleitet ergibt sich
;mit der Kettenregel abgeleitet ergibt sich 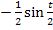 . Das ist, bis auf das Minus, der Zähler des ersten Integranden. Der Nenner des zweiten Integranden ist
. Das ist, bis auf das Minus, der Zähler des ersten Integranden. Der Nenner des zweiten Integranden ist 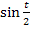 ;mit der Kettenregel abgeleitet ergibt sich
;mit der Kettenregel abgeleitet ergibt sich 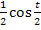 . Das ist exakt der Zähler des zweiten Integranden. Bei beiden Integralen steht also im Zähler die Ableitung des Nenners bzw. das Minus-Eins-fache davon. Wir können beide Integrale mit der Formel
. Das ist exakt der Zähler des zweiten Integranden. Bei beiden Integralen steht also im Zähler die Ableitung des Nenners bzw. das Minus-Eins-fache davon. Wir können beide Integrale mit der Formel 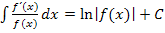 lösen.
lösen.
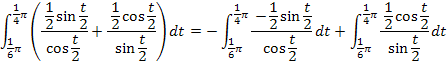
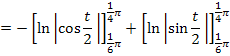
Du kannst jetzt entweder gleich die Grenzen einsetzen, oder noch ein wenig weiter rechnen, um eine etwas elegantere Stammfunktion zu erhalten. Man kann dazu folgende Umformungen vornehmen:
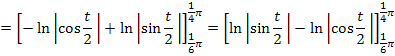
Nun lässt sich das Logarithmus-Rechengesetz 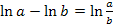 anwenden. Damit erhält man:
anwenden. Damit erhält man:
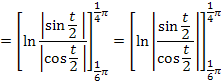
Bekanntlich gilt: 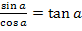
Entsprechend gilt: 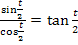
Daher können wir schreiben:
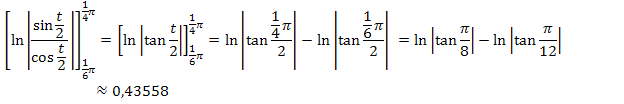
Zu 22b.)
Es soll 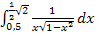 mit der Substitution
mit der Substitution 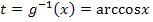 berechnet werden!
berechnet werden!

