Schwierigere Variante der Substitution

Im Prinzip verfahren wir wie bereits bei Teilaufgabe 21a. erläutert, nur jetzt eben mit der Substitution .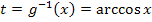

1. Schritt:Substitution 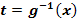und nach x auflösen

Laut Angabe: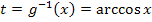

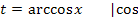
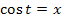
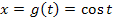
2. Schritt: 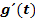bilden

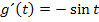
3. Schritt:dx gleich 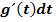setzen

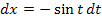
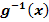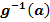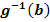4. Schritt:Ursprünglichen Grenzen a und b in einsetzen. Das ergibt die neuen Grenzen und bezüglich t.

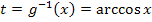
Ursprüngliche Grenzen:0,5 (untere Grenze) und 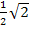(obere Grenze)

Neue untere Grenze: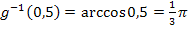

Neue obere Grenze: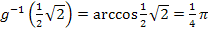

5. Schritt:Ersetze im Integranden (d.h. in der zu integrierenden Funktion) jedes x durch 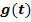und versuche das Integral mit den neuen Grenzen 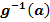und 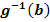zu lösen.

Subst.: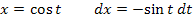

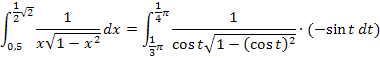
Nun verwenden wir den trigonometrischen Pythagoras, d.h. den folgenden Zusammenhang:

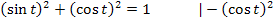
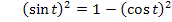
Wir können somit statt dem Ausdruck 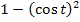, der beim Integranden im Nenner unter der Wurzel steht, einfach 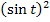schreiben. Dadurch vereinfacht sich das Integral wieder erheblich.

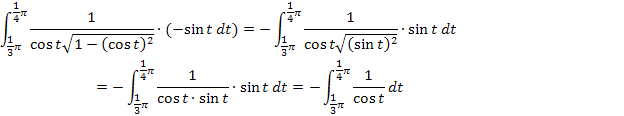
Das neue Integral ist zwar schon viel übersichtlicher, doch leicht zu lösen ist es leider nicht. Wir führen eine zweite Substitution durch:

1. Schritt:Substitution 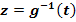und nach t auflösen

Wir wählen .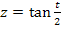

Jetzt kommst du wahrscheinlich total ins Schleudern mit den ganzen Buchstaben.

Im Vergleiche zur „normalen“ Substitution, wo die ursprüngliche Variable x heißt und die neue Variable t, heißt hier die alte Variable t und die neue z. Das t entspricht hier also dem x und der neu eingeführte Buchstabe z dem, was wir sonst t genannt haben.

Somit gilt: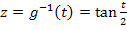

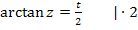
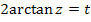
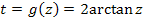
2. Schritt: 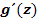bilden

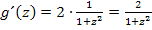
3. Schritt:dt gleich 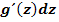setzen

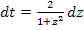
4. Schritt:Grenzen a und b (bezüglich t) in 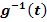einsetzen. Das ergibt die neuen Grenzen 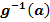und 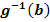bezüglich z.

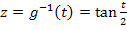
Ursprüngliche Grenzen (bezüglich t): 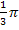(untere Grenze) und 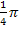(obere Grenze)

Neue untere Grenze (bezüglich z):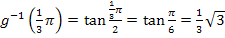

Neue obere Grenze (bezüglich z):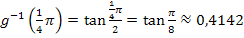

Da sich 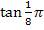leider nicht exakt berechnen lässt, müssen wir zwangsläufig mit 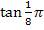als neuer oberer Grenze arbeiten.

5. Schritt:Ersetze im Integranden (d.h. in der zu integrierenden Funktion) jedes t durch 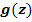und versuche das Integral mit den neuen Grenzen 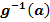und 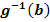zu lösen.

Subst.: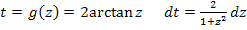

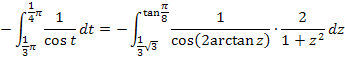
Dieses Integral sieht schrecklich aus, doch lässt es sich mit einigem Rechenaufwand zu einem sehr schönen Integral umformen. Dazu brauchen wir allerdings einige mathematische Formeln. Zur Vereinfachung von verwenden wir die folgende Formel für doppelte Winkel:

Mit erhalten wir:

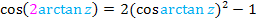
Außerdem gilt:

---